В вышеупомянутых играх с нулевой суммой для двух игроков один из игроков выигрывает то, что проигрывает другой. Сотрудничество или несотрудничество исключены: с точки зрения структуры, это самая простая форма игры («орел или решка» и т. д.). Коммуникация может быть полностью исключена, поскольку главное для обоих игроков – это победа. В данном случае оптимальное решение в любой игровой ситуации – достичь равновесия: максимизировать минимальный достижимый выигрыш. В играх с ненулевой суммой игроки могут улучшить свое положение за счет сотрудничества, но они также могут сделать свою прибыль выше потери противника путем отказа от сотрудничества. На самом деле игры с ненулевой суммой, как правило, преобладают; их привлекательность – в некооперативном поведении. Для стабильного равновесия решающим фактором является доверие между игроками. Однако, по теории игр, игроки рациональны, а доверие, как правило, не будет рациональным решением – эта проблема станет яснее, когда мы перейдем к рассмотрению «дилеммы заключенного». Некооперативное поведение в играх с ненулевой суммой дифференцируется в агрессивные стратегии, направленные на получение незаслуженного преимущества, и слепые стратегии, следующие принципу случайности.
Существует также понятие доминантной стратегии: каждая возможная комбинация стратегий в игре просчитывается каждым игроком в отдельности, и каждый выбирает стратегию, которая обеспечивает наибольшую пользу с его личной точки зрения. Если игрок выбирает одну и ту же стратегию для каждой из возможных комбинаций, она становится его доминантной стратегией в игре: он всегда выбирает один и тот же вариант стратегии в каждой игровой ситуации. Иными словами, оптимальная стратегия с рациональной точки зрения игрока никогда не зависит от стратегии соперника. Избираемый вариант, который не всегда лучше, а, как правило, хуже, чем любая другая стратегия, известен как доминируемая стратегия – таких стратегий следует избегать. Часто игроки не имеют ни доминантных, ни доминируемых стратегий, и в этом случае лучший ответ или стратегия для игрока зависит от выбора противника (то же применимо и в обратном направлении, по отношению к противнику) – так что выбирается иной вариант в зависимости от конкретной ситуации. Равновесие Нэша обеспечивает решение в такой игре, когда возникает комбинация стратегий, в которых выбор каждого игрока является наилучшим ответом на (взятый как данность) выбор соперника – поэтому нет рационального стимула в одностороннем порядке изменить решение или стабильную ситуацию, так как ни один из игроков не извлечет из нее больше выгоды. Это равновесие известно как «принцип лучшего взаимного ответа» и тоже является решением, если оба игрока имеют доминантные стратегии.
В параллельных играх игроки принимают решения одновременно. Поэтому каждый должен оценивать ситуацию с точки зрения другого и пытаться предугадать результат игры. Такой сценарий описывается в матрице игры или решений, в которой противопоставлены варианты стратегии, открытые для игроков в различных ситуациях. В последовательных играх решения принимаются поочередно. Игрок, чья очередь ходить, должен обдумать, как его действие повлияет на действие оппонента. Для иллюстрации этого сценария используются деревья игры, или решений, и ходы изображаются в виде узлов, от которых в разные стороны отходят возможные варианты. На первый взгляд может показаться, что планировать стратегии для параллельной игры труднее. Но если вы когда-нибудь играли в шахматы, то знаете, что последовательная игра тоже невероятно сложна.
Все игры подразделяются на статические либо динамические. Статические игры имеют место единожды, и их можно повторить при прочих равных условиях (например, «орел или решка»). Динамические игры предполагают многочисленные ходы и явно зависят от изменения обстановки и/или от уроков, извлеченных из предыдущих ходов, – поэтому они проходят через несколько хронологических уровней принятия решений. Они могут быть параллельными, последовательными или даже гибридными, то есть параллельно-последовательными.
Чистые стратегии в играх – это однозначные решения за или против возможного хода или серии ходов. Смешанные стратегии оценивают вероятность (в зависимости от индивидуальных предпочтений риска) для каждого возможного варианта стратегии или хода. В игре с полной информацией игроки знают все стратегии и возможные комбинации, а также все возможные выигрыши (платежи) в игре. Эту информацию также называют техническим аспектом игры. Как только она утрачивает актуальность для всех игроков, возникает состояние неполной информации. В реальной экономике компании обычно не имеют полной информации – разве что в плановой.
Если игрок не знает о стратегическом выборе другого игрока, то это игра с несовершенной информацией. Так всегда бывает с параллельными играми. Если, однако, каждый игрок в любое время знает о том, какой стратегический выбор сделали противники, игра обретает состояние совершенной информации – это относится к играм, ходы в которых исключительно последовательны
[80].
«Дилемма заключенного» – пример одновременной игры с ненулевой суммой, отлично иллюстрирующей проблему фундаментальных допущений в теории игр
[81]: двое заключенных, А и В, подозреваются в совершении преступления. Максимальный срок тюремного заключения составляет восемь лет. Судья делает каждому из них следующее предложение: «Если ты свалишь вину на второго парня, выйдешь на свободу, а он получит полный срок. Если вы оба откажетесь говорить, у нас есть достаточно доказательств, чтобы посадить каждого из вас на три года. Если вы оба признаетесь, будете приговорены к пяти годам каждый». Заключенные не могут общаться друг с другом, поэтому у каждого из них есть два варианта: сотрудничать со вторым, то есть молчать, или сдать его, то есть признаться. В результате возникают четыре возможные стратегические комбинации, которые, как правило, изображаются в виде платежной матрицы (или матрицы выигрышей) (табл. 5). В этом случае выигрыш, или минус несколько лет тюрьмы, отрицательный, так как тюремное заключение не обладает положительной полезностью. Первая цифра в скобках – это выигрыш заключенного А, а вторая цифра – выигрыш В.
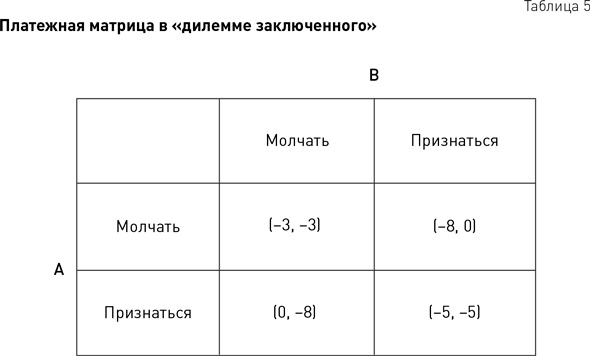
Согласно допущениям теории игр, при принятии решений используется рациональное поведение: каждый игрок хочет максимизировать то, что он лично считает полезным. С позиции А (и с позиции B) в этой ситуации есть два варианта: сотрудничество с другим игроком или предательство. В обоих случаях заключенному выгоднее предать подельника, то есть признаться: нулевой результат лучше, чем –3, а выигрыш в размере –5 лучше, чем –8. Говоря другими словами, свобода лучше, чем три года в тюрьме, а пять лет в тюрьме лучше, чем восемь. Поскольку у обоих игроков одинаковая доминантная стратегия, здесь существует так называемое равновесие доминантных стратегий. Тем не менее в этом случае рациональное поведение приводит к неоптимальному результату, так как оба заключенных признаются и получают по пять лет. Сотрудничество и молчание было бы лучше для обоих, так как им грозил бы только трехлетний срок.



