Более того, в этих условиях детектор в D срабатывает в 2 % случаев – а это просто сумма вероятностей прохождения через А и через В (1 % + 1 %). Значение 2 % не зависит от расстояния между А и В; интерференция исчезает, если в А и В поместить детекторы!
Природа так все устроила, что мы никогда не сможем понять, как она это делает: если мы ставим приборы, чтобы выяснить, по какому пути пойдет свет, – пожалуйста, мы можем это выяснить, но удивительные интерференционные эффекты исчезают. А если у нас нет приборов, показывающих, по какому пути идет свет, интерференционные эффекты восстанавливаются! В самом деле, очень странно!
Чтобы разобраться в этом парадоксе, позвольте напомнить вам самый важный принцип: для того чтобы правильно вычислить вероятность события, нужно очень внимательно отнестись к четкому определению законченного (полного) события – в частности, определить, каковы начальные и конечные условия эксперимента. Вы смотрите на оборудование до и после эксперимента и ищете изменения. Когда мы вычисляли вероятность попадания фотона из S в D без детекторов в А и В, то событием был просто щелчок детектора в D. Если щелчок в D был единственным изменением условий, то нельзя было сказать, по какому пути летел фотон, поэтому возникла интерференция.
Поместив детекторы в А и В, мы изменили задачу. Теперь оказывается, что есть два законченных события – две различные совокупности конечных условий: 1) сработали детекторы в А и D; 2) сработали детекторы в В и D. Если у эксперимента имеется несколько допустимых конечных условий, надо вычислять вероятность каждого как отдельного законченного события.
Для вычисления амплитуды того, что сработают детекторы в А и D, мы умножаем стрелки, которые представляют следующие этапы: фотон летит из S в A; фотон летит из А в D; детектор в D срабатывает. Квадрат длины получившейся стрелки есть вероятность этого события – 1 % – такая, как при закрытом отверстии В, так как в обоих случаях этапы одинаковы. Другое законченное событие – срабатывание детекторов в В и D. Вероятность этого события вычисляется таким же способом, и результат такой же, как раньше – примерно 1 %.
Если нас интересует вероятность срабатывания детектора в D, причем все равно, сопровождается оно срабатыванием детектора в А или в В, то эта вероятность равна простой сумме вероятностей двух событий – 2 %. Вообще, если в системе остается что-то, благодаря чему мы могли бы определить путь фотона, мы имеем различные «конечные состояния» (различимые конечные условия) и складываем вероятности, а не амплитуды всех конечных состояний
[13].
Я указал на эти обстоятельства, потому что чем больше вы наблюдаете странное поведение Природы, тем сложнее построить наглядную модель, объясняющую даже простейшие явления. И теоретическая физика отказалась от этого.
На первой лекции мы увидели, как можно разделить событие на взаимоисключающие пути и как можно «сложить» стрелки для каждого пути. На второй лекции мы узнали, как можно разделить путь на последовательные этапы, как можно представить стрелку для каждого этапа в виде преобразования единичной стрелки и как «перемножить» стрелки для каждого этапа путем последовательных сжатий и поворотов. Следовательно, мы знакомы со всеми необходимыми правилами рисования и соединения стрелок (представляющих кусочки событий) для получения результирующей стрелки, квадрат длины которой является вероятностью наблюдаемого реального события.
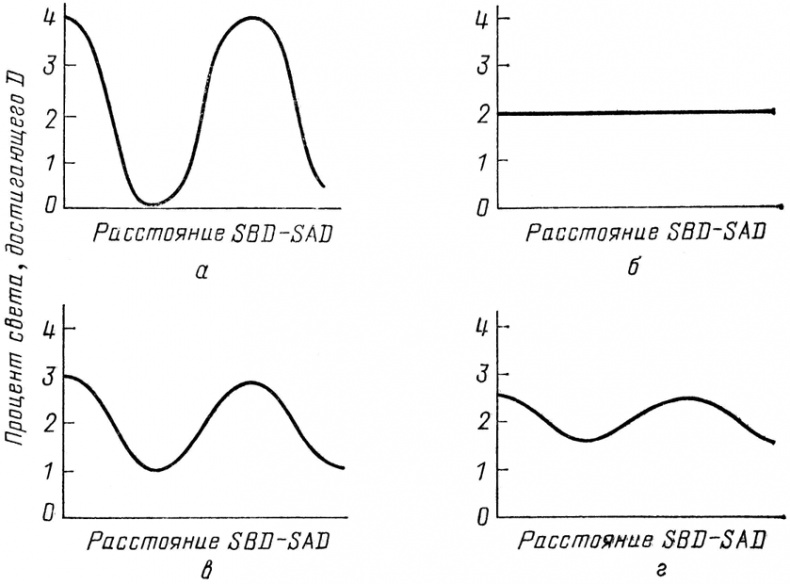
Рис. 51. Если в А и В нет детекторов, возникает интерференция: доля прошедшего света колеблется от 0 до 4 % (а). Если в А и В имеются детекторы, надежные на 100 %, интерференция не возникает – доля попавшего в D света постоянна, 2 % (б). Если детекторы в А и В не надежны на все 100 % (т. е. если иногда в А и В не остается ничего, что можно было бы зарегистрировать), имеются три возможных конечных условия: А и D сработали, В и D сработали, только Dсработал. Окончательная кривая на рисунках обусловлена, следовательно, смесью вкладов всех возможных конечных условий. При уменьшении надежности детекторов в А и В интерференция усиливается. Так, в случае (в) детекторы менее надежны, чем в случае (г). Принцип, которым надо руководствоваться, встретившись с интерференцией, таков: необходимо независимо вычислить вероятность каждого из различных конечных условий путем сложения стрелок и возведения в квадрат длины результирующей стрелки; после этого вероятности складываются обычным образом.
Естественно поинтересоваться, насколько далеко мы можем зайти в этом дроблении события на все более простые подпроцессы. Каков наименьший возможный кусочек события? Имеется ли конечное число кусочков, из которых можно образовать любое явление, связанное со светом и электронами? Имеется ли ограниченное число «букв» в этом языке квантовой электродинамики, комбинируя которые в «слова» и «предложения», можно описать почти каждое явление Природы?
Ответ: да; число равно трем. Существуют только три основных действия, необходимых для получения всех явлений, связанных со светом и электронами.
Прежде чем рассказать вам об этих действиях, мне надо должным образом познакомить вас с действующими лицами. Действующие лица – это фотоны и электроны. Фотоны, частицы света, подробно обсуждались на первых двух лекциях. Электроны были открыты в 1895 г. как частицы: вы могли пересчитать их, вы могли поместить один из них на каплю масла и измерить его электрический заряд. Постепенно стало очевидным, что движение этих частиц объясняет электрические явления в проводах.



