Глава 8
Непостижимая эффективность?
В главе 1 я отмечал, что успех математики в создании физических теорий имеет две стороны – одну я назвал «активной», другую «пассивной». Активная сторона отражает то, что ученые формулируют законы природы в сугубо прикладных математических терминах. То есть они используют математические понятия, соотношения и равенства, иногда – разработанные с прицелом на дальнейшее практическое применение, а иногда – придуманные непосредственно ради конкретной задачи. В таких случаях исследователи обычно полагаются на то, что им представляется, что между свойствами математических понятий и наблюдаемыми феноменами или результатами экспериментов есть определенное сходство. В таких случаях эффективность математики не вызывает особого изумления, поскольку вполне можно сказать, что теории нарочно подогнаны под наблюдения. Однако у активной стороны есть одно удивительное качество – это точность, о которой я еще расскажу в этой главе. «Пассивная» эффективность относится к тем случаям, когда разрабатываются совершенно абстрактные математические теории, безо всякого намерения найти им прикладное применение, однако впоследствии эти теории вдруг превращаются в физические модели с мощными прогностическими способностями.
Ярким примером сочетания активной и пассивной эффективности математики служит теория узлов.
Узлы
Об узлах даже слагают легенды. Наверняка вы помните древнегреческую легенду о Гордиевом узле. Оракул предсказал жителям Фригии, что их следующим царем будет первый, кто въедет в столицу на повозке, запряженной быками. Так царем стал Гордий – землепашец, который, ни о чем не подозревая, въехал в город именно в тот день. Преисполнившись благодарности, Гордий посвятил богам свою повозку и привязал ее к шесту сложнейшим узлом, который никому не удавалось развязать. Затем было получено пророчество, что тот, кто развяжет узел, станет властелином всей Азии. Судьба распорядилась так, что развязал узел (дело было в 333 году до н. э.) не кто иной, как Александр Македонский, и он и в самом деле впоследствии захватил всю Азию. Однако его решение мы не назвали бы ни изящным, ни даже честным: рассказывают, что он просто разрубил узел мечом!
Однако, чтобы познакомиться с узлами, нам не нужно углубляться в историю Древней Греции. Ребенок, завязывающий шнурки, девушка, заплетающая косу, бабушка, вяжущая свитер, моряк, швартующий судно, – все они прибегают к помощи тех или иных узлов. Узлам дают всякие неожиданные названия – «рыбацкий штык», «кошачья лапа», «мартышкина цепочка», «канадская восьмерка», «тещин узел» и «эшафотный узел»
[144]. А в истории морские узлы сыграли такую важную роль, что в XVII веке в Англии им посвятили огромное множество книг. Одну из них, кстати, написал тот самый английский моряк и искатель приключений Джон Смит (1580–1631), который прославился романтическими отношениями с индейской принцессой Покахонтас.
Математическая теория узлов родилась в 1771 году, когда была опубликована статья французского математика Александра Теофила Вандермонда (1735–1796)
[145]. Вандермонд первым понял, что узлы можно изучать в рамках геометрии расположения, иначе называемой топологией, которая изучает исключительно соотношения, зависящие от взаимного расположения, не обращая внимания на размеры и вычисления. Следующим математиком, внесшим вклад в формирование теории узлов, был «Князь математики» немецкий ученый Карл Фридрих Гаусс. В заметках Гаусса содержатся рисунки и детальные описания узлов, а также аналитические исследования их качеств. Однако при всей значимости работ Вандермонда, Гаусса и нескольких других ученых XIX века главный толчок в развитии современной математической теории узлов был сделан с неожиданной стороны – при попытке объяснить структуру вещества. Эта идея зародилась в голове прославленного английского физика Уильяма Томсона, который в наши дни известен как лорд Кельвин (1824–1907). Томсон сосредоточил свои усилия на формулировке теории атомов, основного строительного материала вещества
[146]. Он предложил весьма оригинальную гипотезу: атомы – это узлы, завязанные из трубочек эфира, загадочной субстанции, которая, как тогда полагали, пронизывает все пространство. Согласно этой модели, разнообразие химических элементов как раз и объясняется богатейшим разнообразием узлов.
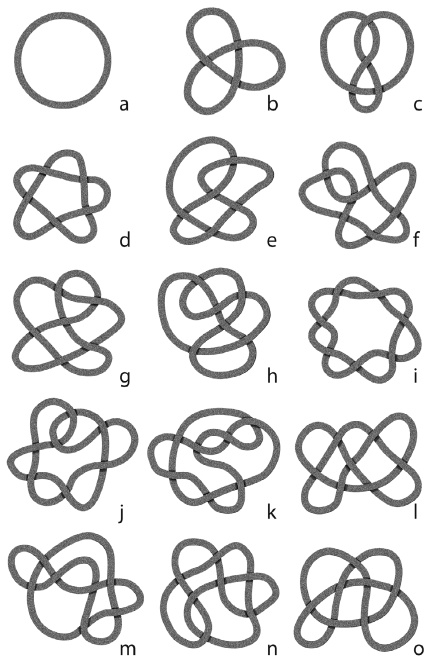
Рис. 54
Если умозаключения Томсона в наши дни и кажутся чистым чудачеством, то лишь потому, что у нас было целое столетие, чтобы принять и экспериментально проверить верную модель атома, в которой электроны вращаются по орбитам вокруг ядер. Однако дело было в Англии в 60-е годы XIX века, и Томсон очень заинтересовался стабильностью сложных колец дыма и их способностью вибрировать – в то время считалось, что эти два качества необходимо учитывать в моделях атомов. Чтобы разработать эквивалент таблицы Менделеева из узлов, Томсон должен был классифицировать узлы, разобраться, какие возможны их виды, и именно необходимость создания такой таблицы и пробудила серьезный интерес к математике узлов.
Как я уже объяснил в главе 1, математический узел выглядит совсем как знакомый каждому узел на шнуре, только концы шнура намертво сращены. Иначе говоря, математический узел изображается замкнутой кривой без свободных концов. Несколько примеров приведено на рис. 54, где трехмерные узлы изображены в виде проекций (теней) на плоскости. Чтобы обозначить положение любых двух участков шнура в пространстве, при пересечении двух участков шнура нижний участок изображается прерванной линией.
Самый простой узел, так называемый тривиальный, или незаузленный узел, – это просто замкнутая кривая без узлов (рис 54, а). Трилистник (рис. 54, b) имеет три пересечения, а восьмерка (рис. 54, с) – четыре. По теории Томсона эти три узла могли, в принципе, служить моделями трех атомов возрастающей сложности – например, атомов водорода, углерода и кислорода соответственно. К тому времени назрела насущнейшая необходимость в создании полной классификации узлов, и за нее взялся друг Томсона, шотландский физик и математик Питер Гатри Тэт (1831–1901).
Когда математики изучают узлы, то задаются примерно теми же вопросами, что и простые смертные, когда смотрят на обычную завязанную веревку или запутанный моток шерсти. Это и правда узел? Эквивалентны ли эти узлы друг другу? Последний вопрос можно переформулировать понятнее: можно ли преобразовать один узел в другой, не разрывая шнуры и не проталкивая один участок шнура сквозь другой, словно сцепленные кольца в руках фокусника? То, насколько это важный вопрос, видно на рис. 55, где показано, как при помощи определенных манипуляций можно получить два совсем разных облика одного узла. В конечном итоге теория узлов ищет способы строго доказать, что те или иные узлы, например трилистник или восьмерка (рис. 54, b и 54, c), и в самом деле разные, игнорируя чисто внешние различия других узлов, например тех двух, которые изображены на рис. 55.



