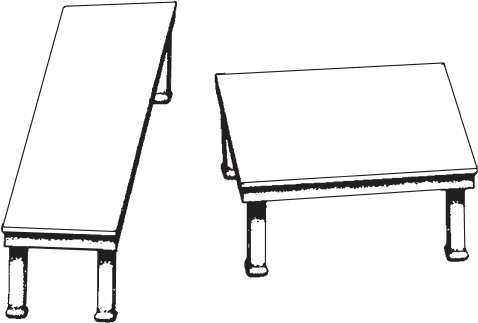
На самом деле нет. Длины этих двух отрезков равны. Глаза правильно сообщают вам, что, если поставить эти два стола в комнате рядом, то левый стол будет намного длиннее, чем широкий (квадратный) правый стол. Но затем мозг преобразует эту правильную информацию в ложную идею: на рисунке длины этих двух отрезков существенно различны. Неправильный вывод очень убедителен, не так ли? Каждый раз, когда я смотрю на этот удивительный рисунок, я все равно не могу в это поверить, и мне приходится по-настоящему их измерять. А затем у меня просто дух захватывает: какую шутку сыграл со мной мозг.
Другая оптическая иллюзия способна убедить нас, что показанные на рисунке прямые линии ну уж никак не параллельны, хотя на самом деле они идеально параллельны. Ниже один из последних чудесных вариантов знаменитой “Иллюзии стены кафе”, обнаруженной в 1973 году британскими психологами Ричардом Грегори и Стивом Симпсоном на стене кафе в английском Бристоле. Параллельные линии? Ну уж нет!!! Но они параллельны!!!

Кажется, что на рисунке внизу мы видим вращающиеся, как шестеренки, круги. Если очень внимательно присмотреться к одному из них, можно заметить, что он вообще не вращается, но затем вы разочарованно заметите, что вращаются все остальные круги! Это классическая оптическая иллюзия, показывающая, что вашему мозгу – и моему, и мозгу каждого – не удается правильно проанализировать информацию на рисунке.


И еще одна невероятно искусная иллюзия способна убедить нас, что на рисунке изображены два предмета разных цветов, хотя на самом деле они одного и того же цвета. Хотите верьте, хотите нет, но верхняя и нижняя половинки этого объекта, обозначенные буквами A и B, одного цвета. Чтобы проверить, что это невероятное утверждение правильно, потребуется закрыть на рисунке все, кроме объекта (включая середину, где половинки “крепятся” друг к другу), поскольку, если этого не сделать, мозг будет продолжать настойчиво убеждать вас, что эти половинки совершенно разного цвета.
Именно по этим причинам мы нуждаемся в инструментах, помогающих нам понять, каков на самом деле окружающий нас мир, – инструментах, более надежных, чем одни только наши ощущения и наш доверчивый мозг.
Синестезия
Иногда наш мозг совмещает элементы информации и затем, творчески их используя, делает удивительные выводы, не имеющие под собой никакой реального основания. Классический пример – рисунок, на котором изображены две фигуры. Назовем их “Кики” и “Буба” [“Мума”]. Посмотрите на две фигуры и скажите мне, какая из них “Кики”, а какая “Буба”.
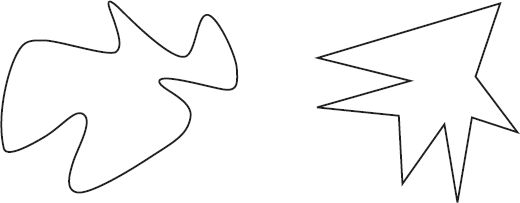
Практически каждый, кто смотрит на эти фигуры, убежден: слева “Буба”, а справа “Кики”. Но какие для этого могут быть резоны? На картинке нет и намека на то, с чем мы имеем дело в обычной жизни, и названия фигур – просто бессмысленные слова. Тогда, скажите на милость, что заставляет с такой уверенностью говорить, что одно из слов должно быть названием одной фигуры, а другое – другой?
Рационального объяснения нет. Это связано только с тем, что для всех звук “Буба” звучит мягче и круглее, чем “Кики”, который кажется более колючим и угловатым. И мы склонны видеть слева более мягкую и круглую картинку, а справа – более колючую и угловатую.
Такого рода связь между звуками и формами и является одной из разновидностей синестезии, которая означает смешение ощущений, происходящих от различных органов чувств. Другой пример синестезии – это ощущение наличия связи между отдельными цифрами и цветами, знакомое многим людям. Например, цифра 7 может для вас ассоциироваться с синим цветом, 3 – с желтым и так далее.
Дэниел Таммет – хорошо известный пример человека с синестезией. Он помнит и может воспроизвести иррациональное число π с точностью до 20000 знаков после запятой (3.14159265358979323846264…). В своей книге “Рожденный в синий день”
[53] он объясняет, что, для того чтобы запомнить так много цифр, он не думает о самих цифрах, скорее они предстают перед его мысленным взором как последовательности цветов и холмистые пейзажи.
Мозг часто дурачит нас подобным образом, а мы даже не подозреваем об этом. И иллюзии не всегда связаны с сенсорным восприятием. Наш бедный мозг можно одурачить многими разными способами. Это одна из причин, почему столь важно использовать научные методы и двойные слепые тесты.
Эффект якоря
Даниэль Канеман, израильско-американский психолог, занимался вопросом о том, как мы принимаем решения и как на нас можно влиять в процессе принятия решения. (Сейчас Канеман, родившийся в 1934 году, почетный профессор Принстонского университета. В 2002 году он стал лауреатом Премии по экономике памяти Альфреда Нобеля “за применение психологической методики в экономической науке, в особенности при исследовании формирования суждений и принятия решений в условиях неопределенности”.) Так называемый эффект якоря – один из открытых и изученных им психологических феноменов. Оказывается, всякий раз, пытаясь оценить какие-то числовые значения, мы подсознательно можем “привязать” свой ответ к числам, которые мы видели раньше, даже если эти числа не имеют никакого отношения к рассматриваемому вопросу.
Классический эксперимент с рулеткой – один из примеров, демонстрирующий необъективность такого рода
[54]. В этом эксперименте испытуемому задается вопрос, ответ на который должен быть числом между 1 и 100. Например, такой: “Какой процент всех государств мира расположен в Африке?” (При этом принципиально важно, чтобы человек не знал ответ и должен был его угадать.) Прежде чем задать вопрос испытуемому, ему предлагают запустить рулетку (большинство соглашается). Обычная рулетка останавливается на произвольном числе между 1 и 100, однако эта устроена так, что стрелка может останавливаться только на 16 или 45. Эксперимент повторяется много раз с большим числом испытуемых (скажем, 1000 человек). Это значит, что до ответа на вопрос приблизительно у 500 человек, запускавших рулетку, выпадает 16, а у других 500 испытуемых – 45.







