Но какие вопросы следует задавать пикселям, если мы хотим определить, к какой части тела они принадлежат? В прошлом нам пришлось бы самим придумывать хитрую последовательность вопросов, которая позволила бы решить эту задачу. Но нельзя ли запрограммировать компьютер так, чтобы он нашел нам лучшие вопросы для ее решения? Взаимодействуя со все новыми данными – все новыми изображениями, – он находит набор вопросов, по-видимому наиболее эффективно приводящий к ответу. Именно так и работает машинное обучение.
Чтобы этот процесс не был обучением с совершенно чистого листа, нужно начать с каких-то вопросов-кандидатов, которые, как нам кажется, могли бы привести к решению задачи. Обучение происходит путем уточнения наших идей с формированием из них действенной стратегии. Какие же вопросы, по вашему мнению, могли бы помочь нам отличить руку от макушки?
Обозначим пиксель, который мы хотим распознать, буквой Х. Компьютеру известна глубина каждого пикселя, то есть его удаленность от камеры. Хитрая стратегия, которую придумали в Microsoft, состоит в «опросе» окружающих его пикселей. Например, если Х – пиксель, находящийся на макушке, то пиксели, расположенные выше Х, с гораздо большей вероятностью не будут относиться к телу и, следовательно, должны иметь большую глубину. Если же взять ближайшие к Х пиксели, расположенные ниже его, они должны быть пикселями лица и их глубина должна быть близка к глубине пикселя Х. Но если этот пиксель относится к руке, а рука эта вытянута, тогда будет существовать ось, направленная вдоль этой руки, по которой глубина будет оставаться практически неизменной, но смещение перпендикулярно этой оси будет быстро выводить пиксели за пределы тела – на стену, находящуюся на фоне изображения. Такие последовательно накапливающиеся – кумулятивные – вопросы о глубине окружающих пикселей могут позволить понять, к какой части тела принадлежит данный пиксель.
Такой кумулятивный опрос можно представить себе как процесс построения дерева решений. Каждый следующий вопрос образует новую ветвь этого дерева. Сначала алгоритм выбирает случайный набор исходных направлений и некое случайно взятое пороговое значение глубины: например, двигаться вверх; если изменение глубины меньше у, переходить на левую ветвь дерева решений; если больше – на правую ветвь и так далее. Мы хотим найти такие вопросы, которые дают новую информацию. Стартовав со случайного исходного набора вопросов и применив их к 10 000 помеченных изображений, мы начинаем получать некоторые результаты. Например, мы знаем, что пиксель Х на изображении 872 относится к локтю, а на изображении 3339 – к левой ступне. Каждую ветвь или каждую часть тела можно считать отдельной корзиной. Мы хотим, чтобы наши вопросы обеспечивали попадание всех изображений, на которых пиксель Х относится к локтю, в одну и ту же корзину. Вряд ли так получится при применении первого, случайного набора вопросов. Но с течением времени, по мере того как алгоритм начнет уточнять углы и пороговые уровни глубины, он станет все лучше распределять пиксели по корзинам.
Повторяя этот процесс, алгоритм изменяет значения и совершенствуется в различении пикселей. Важно помнить, что мы не стремимся добиться абсолютного совершенства. Если в конце концов в корзине оказываются 990 из 1000 изображений, на которых пиксель Х относится к локтю, это означает, что алгоритм распознает нужный элемент изображения в 99 % случаев.
К тому времени как алгоритм находит оптимальный набор вопросов, программисты уже понятия не имеют, как именно он пришел к этому выводу. Они могут посмотреть на любую точку дерева и увидеть, какие вопросы задаются перед нею и после нее, но дерево содержит в целом более миллиона разных вопросов и все они хоть немного, но отличаются друг от друга. Восстановить логику задним числом, понять, как именно алгоритм решил, что в данной точке дерева следует задать именно этот вопрос, очень трудно.
Представьте себе, что вы пытаетесь запрограммировать подобную систему вручную. Вам пришлось бы придумать более миллиона разных вопросов. Эта перспектива обескуражила бы и самых отважных из программистов, а вот компьютер справляется с такого рода числами легко и непринужденно. Удивительно, что эта система работает настолько хорошо. Программистам потребовалось приложить некоторые творческие усилия, чтобы поверить, что вопросов о глубине соседних пикселей действительно может быть достаточно, чтобы определить, на какую часть тела мы смотрим, – но вся последующая творческая работа была выполнена машиной.
Одной из проблем машинного обучения является так называемая «переподгонка»
[27] (overfitting), или переобучение. Всегда можно придумать достаточно вопросов, чтобы распознать изображение по тренировочным данным, но не хотелось бы получить программу, слишком привязанную к тем данным, на которых она обучалась. Она должна уметь извлекать из этих данных нечто применимое в более широкой области. Пусть, например, мы пытаемся создать набор вопросов для идентификации граждан; у нас есть для этого имена и номера паспортов 1000 человек. Мы можем спросить: «Номер вашего паспорта – 834765489? Тогда вы, вероятно, Ада Лавлейс». Этот метод будет работать на имеющихся данных, но окажется совершенно непригоден за пределами исходной группы, так как ни у кого из граждан, не принадлежащих к ней, не будет паспорта с таким номером.
Если на графике имеются десять точек, можно задать функцию, кривая которой проходит через все эти точки. Нужно всего лишь уравнение с десятью членами. Но это не покажет закономерностей, скрытых в данных, а именно они могут быть полезны для понимания новых точек графика. Чтобы избежать такой переподгонки, нужно уравнение с меньшим количеством членов.
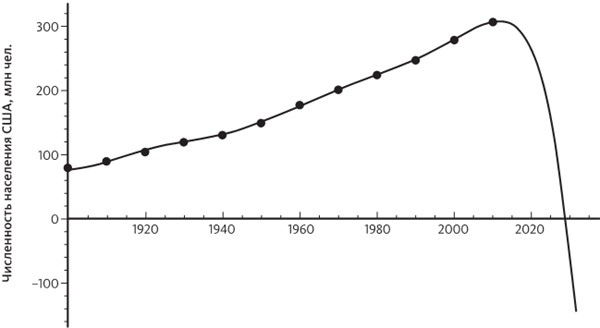
Иногда переподгонка не позволяет увидеть общие тенденции, заставляя нас моделировать слишком мелкие подробности, и это приводит к получению совершенно диких предсказаний. Ниже приведен график, двенадцать точек которого показывают численность населения США с начала прошлого века. Общая тенденция лучше всего описывается квадратным уравнением, но нельзя ли использовать функцию с более высокими, чем х2, степенями х? Если взять полином степени х11, он позволяет получить чрезвычайно точное соответствие данным, но при продолжении этой функции в будущее она резко падает, предсказывая полное вымирание населения США к середине октября 2028 года. Возможно, математике известно нечто такое, о чем мы не знаем?
Алгоритмические галлюцинации
Успехи, достигнутые за последние пять лет в области компьютерного зрения, поразили всех. Причем новые алгоритмы способны ориентироваться не только в изображениях человеческого тела. Достижение способности декодировать визуальные образы, сравнимой с той, которой обладает человеческий мозг, было трудной задачей для любого компьютера, претендующего на роль конкурента человеческого разума. Цифровая видеокамера может зафиксировать изображение в таких подробностях, сохранение которых далеко превосходит возможности человеческого мозга, но это не значит, что такая камера способна извлечь из миллионов пикселей связное изложение. Мы все еще далеки от понимания того, как именно мозг обрабатывает данные и объединяет их в единую концепцию, не говоря уже о воспроизведении этого процесса в наших кремниевых друзьях.



