рассчитывал получить 57 000 руб.;
получил гитару и часы, 24 000 + 58 000 = 82 000 руб.
Разницу 82 000 – 57 000 = 25 000 руб. он должен положить на стол.
Теперь на столе лежит сумма 10 000 + 25 000 = 35 000 руб.
Из этих денег надо часть отдать первому брату, чтобы в итоге он получил то, на что рассчитывал: 50 000 (на это он рассчитывал) – 30 000 (полученная им видеокамера) = 20 000 руб.
В результате на столе останется сумма 35 000 – 20 000 = 15 000 руб. Остаток следует разделить поровну между тремя братьями, в итоге каждый получит 15 000/3 = 5000 руб.
Итак, первый брат рассчитывал получить 50 000 руб., а получил 30 000 (видеокамера) + 20 000 (из общей суммы) и еще 5000 руб. (после деления остатка) = 55 000 руб.
Второй брат рассчитывал получить 55 000 руб., а получил 65 000 (акваланг) + 5000 (после деления остатка) – 10 000 (то, что он положил деньгами на стол) = 60 000 руб.
Третий брат рассчитывал получить 57 000 руб., а получил 24 000 (гитара) + 58 000 (часы) + 5000 (после деления остатка) – 25 000 (то, что он положил деньгами на стол) = 62 000 руб.
Таким образом, каждый брат получил на 5000 руб. больше, чем рассчитывал, и использование этой схемы раздела всегда дает подобный результат. Итак, сформулированное нами ранее требование справедливого деления соблюдено, каждый получил больше того, на что рассчитывал, все получили одинаковую "доплату сверху". Схема достаточно гибкая, братья могут заранее договориться, что покажут друг другу предварительные оценки, после чего у каждого есть право их подкорректировать. Допустим, двое из братьев хотят непременно получить акваланг – не денежный эквивалент, а сам предмет. В таком случае они могут поторговаться, повышая цену, поскольку вещь, по правилам этой схемы, достанется тому, чья цена окажется выше. При этом каждый понимает, что, если он хочет, чтобы вещь досталась именно ему, он должен завысить цену, но ему придется выложить на стол бóльшую разницу.
Эта схема расчета приведет к нужному результату при любом числе братьев, количестве наследуемых предметов и при любых оценках стоимости вещей. Естественно, перед проведением такого расчета все братья должны ознакомиться с системой расчета и должны быть с ней согласны.
Обратите внимание на разницу цены, назначенной братьями для гитары. Можно предположить, что третьему брату она дорога как напоминание о детстве и он хочет оставить ее непременно себе. Как видите, в стоимость предмета входит оценка в рублях такой "тонкой материи", как воспоминания детства. В этом нет ничего удивительного. Например, вам предлагают выполнить какую-то работу за определенную сумму. Выполнение работы связано с необходимостью контактировать с неприятными людьми или, например, вас ждет ненормированный рабочий день, да еще с длительными ночными поездками. Вы говорите себе: "Не нужны мне эти не такие уж большие деньги, спокойствие дороже!" Это вы произвели оценку. Свое спокойствие вы оценили в бóльшую сумму, чем та, которую получите за работу. А сколько же стоит ваше спокойствие? Его можно оценить той суммой, за которую вы все же согласились бы выполнить эту работу. Теоретически такая сумма – возможно, гигантская – всегда существует.
Предложенная система справедливого деления достаточно универсальна. Если бы три женщины из предыдущего раздела указали свои оценки трех кусков мяса, в итоге после расчета по такой схеме каждая получила бы больше, чем рассчитывала.
Можно обойтись без денежного выражения
Методика справедливого раздела может быть использована и при решении некоторых проблем, возникающих в научной практике. Возьмем для примера многостадийный органический синтез – например, получение уксусной кислоты CH3COOH из метана CH4. На самом деле уксусную кислоту никто так не синтезирует, в промышленности ее получают окислением бутана С4Н10 или взаимодействием метанола СН3ОН с монооксидом углерода СО. Однако выберем необычный способ синтеза, а заодно убедимся, что он осуществим.
Рассмотрим все стадии процесса. Вначале бромированием получаем из метана бромметан:
Затем проводим взаимодействие бромметана с металлическим магнием, который «встраивается» между углеродом и бромом. Образуется магнийорганическое соединение (реактив Гриньяра). Реакция проводится в диэтиловом эфире:
На следующей стадии полученный реактив Гриньяра взаимодействует с углекислым газом СО2, который «встраивается» между углеродом и магнием:
CH3MgBr + CO2 = CH3C(=O)OMgBr
Последняя стадия: при взаимодействии соединения, полученного на предыдущей стадии, с HBr, образуется уксусная кислота и побочный продукт MgBr2:
CH3C(=O)OMgBr + HBr = CH3COOH + MgBr2
Вся работа достаточно трудоемкая, поскольку, помимо проведения четырех основных стадий, необходимо предварительно очистить исходные соединения и растворители, а также отделить побочные продукты реакций.
Предположим, что получение большого количества конечного продукта будет оплачено. Общая стоимость работы для решения нашей задачи значения не имеет, и мы не будем ее рассматривать. Чтобы успеть все сделать к назначенному сроку, вы берете себе в помощники еще двух химиков. Опыт экспериментальной работы у всех троих одинаков, каждый сможет провести любую из показанных выше стадий. Поэтому все трое решили поделить заработанную сумму на три равные части. Теперь надо разделить объем работы также на три равные части.
Несмотря на то что мы решили обойтись без денежного выражения объема работы на каждой стадии, мы постараемся соблюсти принцип справедливого раздела. Сформулируем его несколько иначе – в сравнении с тем, который применялся при разделе наследства. Каждому химику нужно предоставить возможность выполнить объем работы меньший, чем одна треть (по его собственной оценке) общего объема. Объединим все участвующие в синтезе соединения, затем дадим каждому из участников независимо друг от друга провести деление всего объема работы на три равные части с помощью вертикальных черточек. Первый участник проводит деление сплошными вертикальными линиями, второй – пунктирными, третий – волнистыми.
Вот вариант деления всего объема работы на равные части, предложенный первым химиком (рис. 10.3).
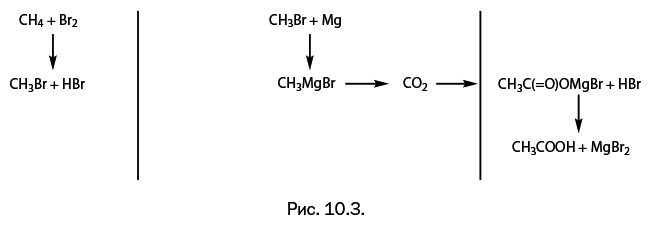
С точки зрения второго химика, деление работы на три равные части выглядит следующим образом (рис. 10.4).

