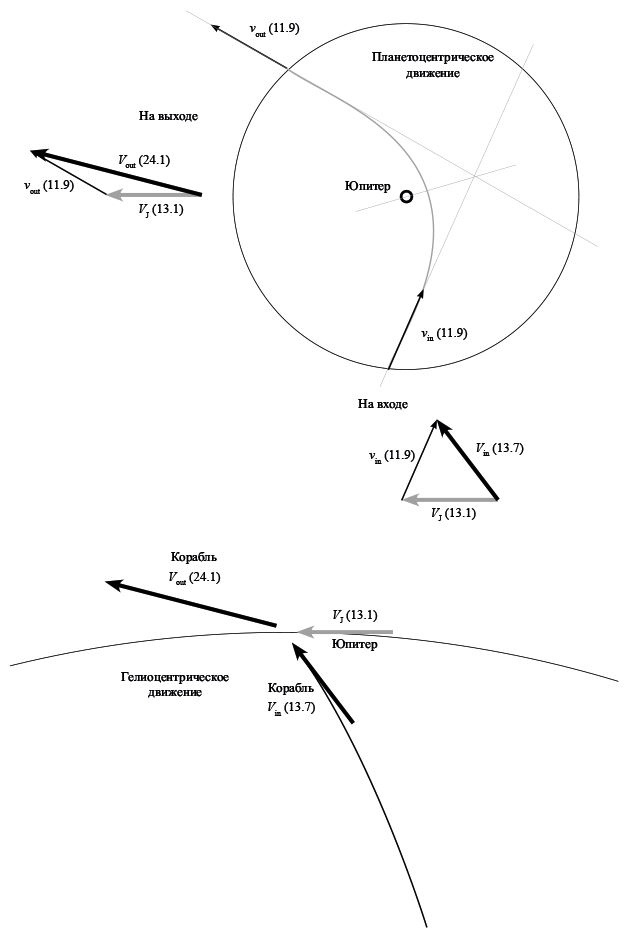
На входе в сферу действия мы имеем скорость корабля в гелиоцентрической системе отсчета. Зависимость ее от конкретной точки входа довольно существенна, но на ход рассуждений это не влияет. Примем, что точка входа находится в ближайшей к Солнцу части сферы действия, где скорость корабля составляет 13,7 км/с. Орбитальная скорость Юпитера в этой же системе близка к 13,1 км/с. Чтобы определить начальные условия полета относительно планеты, мы должны вычесть из вектора нашей гелиоцентрической скорости на входе вектор скорости Юпитера – честно нарисовать треугольник скоростей и найти их разность по правилам векторной алгебры. Учитывая, что угол между двумя векторами в нашем случае близок к 53°, планетоцентрическая скорость корабля составит 11,9 км/с.
В пределах сферы действия мы движемся по гиперболической орбите относительно Юпитера, параметры которой определяются вектором состояния (три координаты и три компоненты скорости) в точке входа. По гиперболической – потому что пришли из бесконечности с ненулевой относительной скоростью и имеем положительную полную энергию относительно планеты. Нельзя оказаться на орбите вокруг Юпитера или любой другой планеты без специальных ухищрений!
Результат облета сильнее всего зависит от положения точки входа, которое задается предшествующей межпланетной траекторией и проведенными на подлете коррекциями. Чем ближе к планете мы пролетим, тем сильнее ее тяготение завернет нашу траекторию. К примеру, мы могли подходить с таким расчетом, чтобы траектория полета указывала на точку правее Юпитера на 15 его радиусов – эта величина называется прицельной дальностью. В реальности минимальное расстояние от центра планеты будет намного меньше, и, если прицельная дальность выбрана неправильно, мы можем столкнуться с планетой. Но мы взяли прицельную дальность с запасом, а потому благополучно огибаем Юпитер и возвращаемся к границе сферы действия, имея ту же самую величину скорости 11,9 км/с, что и при входе, но другое направление полета. Заходили вдоль одной асимптоты гиперболы, выходим вдоль второй.
Мы прощаемся с планетой, для чего векторно складываем с нашей новой скоростью относительно Юпитера скорость планеты относительно Солнца. Последняя имеет прежнюю величину и лишь слегка отклонилась по направлению – мы считаем, что пролет длился недолго по сравнению с периодом обращения планеты, и на самом деле так оно и есть. Однако направление отлетной скорости сильно изменилось: в нашем случае корабль повернул на 84° влево. Треугольник скоростей выглядит совсем иначе, и мы заканчиваем сближение с иной гелиоцентрической скоростью и по величине, и по направлению, нежели скорость входа. Теорема косинусов подсказывает, что величина скорости относительно Солнца увеличилась до 24,1 км/с!
Да, скорость корабля увеличилась на 75 % – и это произошло оттого, что мы позаимствовали немного энергии у Юпитера и чуть-чуть притормозили его орбитальное движение. В общем случае могло быть и наоборот – мы отдали бы часть энергии планете, а сами замедлились. Достаточно интересно «поиграть» с этими векторами, считая задачу двумерной и рассматривая события «сверху», со стороны Северного полюса мира. Несложно показать, что при облете планеты с задней полусферы корабль выйдет с большей скоростью, чем имел на входе, а с передней – наоборот.
Самый первый пертурбационный маневр в истории космонавтики был выполнен в ходе полета советской межпланетной станции Е-2А («Луна-3»), запущенной 4 октября 1959 г. на сильно вытянутую эллиптическую, почти параболическую орбиту спутника Земли. Выполняя облет Луны с целью фотографирования ее обратной стороны, станция затормозила, изменила свою траекторию на чисто эллиптическую меньшего размера и вернулась затем к Земле с направления, благоприятного для передачи изображений. Этот полет стал возможным в результате пионерских работ В. А. Егорова, М. Л. Лидова, Д. Е. Охоцимского и их коллег из Математического института АН СССР, выполненных в 1957 г. под руководством академика М. В. Келдыша.
В США к идее гравитационных маневров пришли своим путем.
Летом 1961 г. в Группе траекторий Лаборатории реактивного движения (Jet Propulsion Laboratory, JPL) стажировался 26-летний студент-математик из Калифорнийского университета в Лос-Анджелесе Майкл Эндрю Минович. Решив поставленную перед ним конкретную математическую задачу определения параметров траектории полета в поле тяготения между двумя заданными точками при фиксированном времени перелета, он заинтересовался проблемой расчета траектории КА, выполняющего облет Марса с последующим возвращением к Земле. Будучи одним из вариантов ограниченной задачи трех тел, аналитического решения она не имела, а численный расчет на имеющемся в JPL компьютере IBM 7090 сходился далеко не всегда.
Минович придумал способ приближенной оценки параметров облетной траектории, пригодных для дальнейшего численного расчета, и заметил интереснейшую вещь: энергия КА после сближения с планетой – если измерять ее в системе отсчета, связанной с Солнцем, – может очень значительно отличаться от энергии до сближения.
В августе Майкл подготовил 47-страничный доклад с алгоритмом расчета траекторий в случае последовательного пролета нескольких планет. Молодой автор показал, что, войдя с нужного направления в поле тяготения планеты, можно «позаимствовать» часть ее энергии и выйти в другом направлении со значительно большей энергией и гелиоцентрической скоростью. В частности, на выходе можно получить направление и скорость, позволяющие направить аппарат к другой, более далекой планете. При этом скорость отлета от Земли может оказаться меньше, а время перелета – короче, чем если бы аппарат сразу запускался ко второй планете. Аналогичный «фокус» можно проделать и у второй планеты – и направиться к третьей. В качестве иллюстрации Минович предложил для расчета траекторию Земля – Венера – Марс – Земля – Сатурн – Плутон – Юпитер – Земля.
Руководитель Майкла встретил эту инициативную работу без энтузиазма, и Миновичу пришлось самостоятельно программировать свои уравнения и вводить исходные данные – координаты девяти планет на 1960–1980 гг. Он проводил расчеты с января 1962 по сентябрь 1964 г. на институтском компьютере, а с июня 1962 г. и на машинах в JPL, после того как продемонстрировал руководителю Группы траекторий Виктору Кларку свои результаты расчета траектории Земля – Венера – Марс – Земля и получил поддержку.
В марте 1963 г. Минович представил в JPL официальный отчет на 130 страницах уже с конкретными вариантами траекторий Земля – Венера – Меркурий и Земля – Венера – Марс. Среди них, в частности, была и та трасса, по которой спустя десять лет проследовала американская АМС «Маринер-10» (Mariner 10). Она была запущена 3 ноября 1973 г. и совершила 5 февраля 1974 г. пролет Венеры, благодаря которому была направлена к своей главной цели – Меркурию. Это и был первый гравитационный маневр в американской космической программе.
Весной и летом 1963 г. Минович выступил с несколькими докладами, после чего его работа стала хорошо известна в профессиональной среде, а метод взят на вооружение. Практическое использование «планетной» тяги поначалу казалось затруднительным из-за высокой чувствительности метода к погрешностям траекторий, но в начале 1965 г. Эллиотт Каттинг и Фрэнсис Стёрмс показали, что с использованием существующей навигационной аппаратуры необходимые точности достижимы.



