Немного практики
Установите, где определение, суждение, умозаключение.
14.1. Южный город.
14.2. Я имею права.
14.3. Раз он вызвался, то пусть и делает.
14.4. Самый технологичный завод.
14.5. Самый технологичный завод находится в Японии.
14.6. Морозы.
14.7. Наступили морозы.
14.8. Светает.
14.9. Дееспособность.
14.10. Бездействие.
14.11. Неверно, что это квадрат.
14.12. Это круг.
14.13. Моя ответственность.
14.14. Москва — столица России.
14.15. Этот предмет красный. И этот предмет красный. Значит, оба предмета красные.
Глава 15
Понятие и определение. Круги Эйлера
Чтобы погрузиться в науку логику, для начала определим основополагающие понятия. Вот с самого «понятия» и «определения» и начнем. Без грамотного понимания и определения явления или события невозможно разобраться с логикой рассуждений и уяснить их смысл.
Что подразумевает человек, когда произносит какие-либо слова? Что он имеет в виду? Можно ли понять смысл предложения, если в нем есть неизвестное нам слово? Что конкретно имеет в виду человек, когда произносит, например, слово «право»? Имеет ли он в виду общепринятое широкое значение или узкое юридическое? Без понятий и определений мы не смогли бы понимать друг друга. Мы все прекрасно понимаем значение таких слов, как «окно», «компьютер», «собака», «карандаш», «стол». Но задумайтесь, можете ли вы точно дать определения таким терминам, как «справедливость», «инфляция», «возможность», «время»? Это уже гораздо сложнее. Или даже взять элементарные и знакомые всем с детства слова «красный», «теплый», «мягкий». Как их объяснить словами, без демонстрации?
Итак, об этих базовых элементах мышления, фундаменте логики мы и поговорим. Начнем с термина «понятие», а потом перейдем к термину «определение». Мы все мыслим с помощью понятий. Понятием называется форма мышления, которая обозначает какой-либо объект или его свойство. Вокруг нас бесчисленное множество разных объектов, и каждый из них отражается в нашем сознании как какое-либо понятие. Просто оглянитесь вокруг. Вы видите горы, реки, облака, светящее солнце? А может быть, стол, лампу, календарь и ручку с блокнотом? Каждому объекту или явлению в этом мире мы задаем свои имена. Вот такие имена в логике и называют «понятие». Мы анализируем разные предметы, сравниваем их с другими, выявляем их различные свойства и характеристики, объединяем разные предметы в группы на основании сходных принципов, для того чтобы сформировать их мысленные образы: это всё «фрукты», а это «цитрусовые», из них вот это «мандарины», это «грейпфруты», а это «апельсины».
Только подумайте: в объективной реальности никаких понятий нет. Это все плод человеческого разума и воображения, так люди договорились между собой. Все, что мы называем, существует лишь в нашей голове. Нет в объективном мире никаких «прав» и «свобод», нет «демократии» и «денег», нет «юристов» и «учителей», «бакалавров» и «специалистов», не существует «хордовых» и «одноклеточных». Есть понятия, к которым мы обращаемся, чтобы не только общаться и понимать друг друга, но и чтобы наш мозг составил правильную картину окружающего мира.
Не стоит путать «слово» и «понятие»: это все-таки разные вещи. Понятия выражаются словами. Иногда одним словом могут выражаться разные понятия.
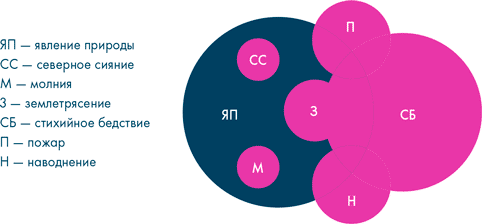
Чтобы проиллюстрировать это наглядно, предлагаю обратиться к так называемым кругам (или диаграммам) Эйлера
[261]. Если вы думаете, что ничего не знаете о кругах Эйлера, то глубоко ошибаетесь, потому что каждый хоть раз в жизни видел их в виде интернет-мемов.
Леонард Эйлер (1707–1783) — известный швейцарский, немецкий и российский математик, член Петербургской академии наук. Он придумал использовать простую визуализацию для обозначения объема понятий и множеств элементов. Круги Эйлера просты и наглядны, они очень упрощают рассуждения и именно поэтому так часто используются в логике, математике, статистике и менеджменте. Они отлично показывают, в каких логических взаимоотношениях могут быть те или иные понятия. Давайте посмотрим, какие возможны варианты таких взаимоотношений понятий.
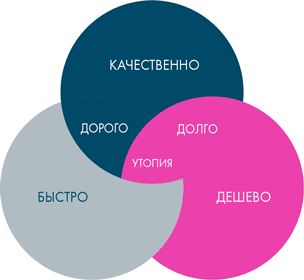
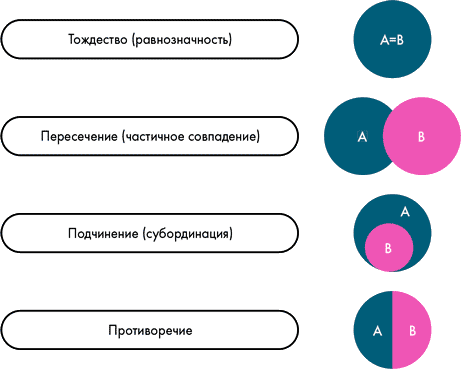
Тождество — в данном случае понятия подразумевают один и тот же предмет. Например, А = квадрат, В = равносторонний прямоугольник; А = Москва, В = столица России; А = лучший тренер по технологиям убеждения, В = Никита Непряхин. Ладно, шучу.
Пересечение — в таких случаях объем одного понятия частично входит в объем другого понятия. Например, А = студент, В = спортсмен. Действительно, часть студентов могут быть спортсменами, а часть — нет. И наоборот, кто-то из спортсменов может учиться в вузе, а кто-то нет. Или: А = мужчина, В = врач. Кто-то из мужчин действительно работает врачом, но какая-то часть врачей — явно женщины. Может быть, и бо́льшая.
Подчинение — в этих случаях одно понятие включает в себя другое. Например, А = верующий, В = православный. Все православные — верующие. Но среди верующих есть еще и католики, и протестанты, и буддисты, и мусульмане. Или: А = цитрусовые, В = апельсин; А = растение, В = береза.
Противоречие понятий представляет собой отрицание одним понятием другого. Например, А = низкий, В = высокий; А = работающий, В = безработный; А = черный, В = белый и т. д.
Давайте рассмотрим несколько примеров использования кругов Эйлера, но уже более сложные варианты.
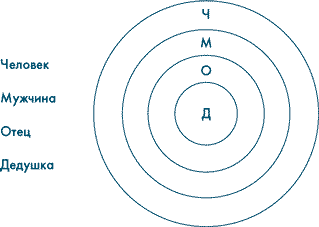
Что мы видим из схемы, в которой продемонстрировано последовательное подчинение? Каждый мужчина — человек. Но не каждый человек — мужчина. Любой отец — мужского пола. Но не каждый мужчина успел обзавестись потомством. Не каждый отец является дедушкой. При этом любой дедушка всегда является также отцом.