Анализируя эти два примера, мы прекрасно понимаем, что вероятность этих событий отличается. Если я несколько раз каким-то невероятным образом мог избежать серьезных травм в результате падения с третьего этажа, это вовсе не означает, что в следующий раз все будет также хорошо. В то же время мы понимаем, что если тетя 35 лет подряд ездит на Новый год к родственникам, то, скорее всего, она и в этом году к ним поедет. Конечно, ей могут помешать форс-мажорные обстоятельства, но объективных препятствий для совершения события мы пока не видим. Вероятность — высокая.
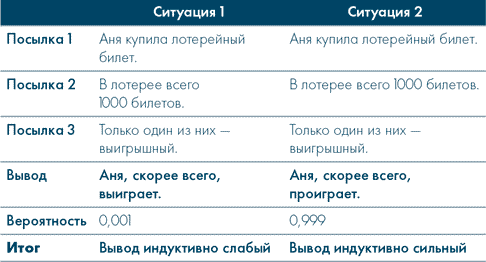
Давайте представим: какой шанс выиграть главный приз в лотерею, если из тысячи выпущенных билетов выигрывает только один? Это означает, что шанс один из тысячи, то есть вероятность выигрыша близка к нулю. Можно ли считать это умозаключение верным: «Мой друг выиграл в лотерею, значит, и у меня есть большой шанс стать победителем»? Конечно, индуктивная сила этого рассуждения минимальна, оценка — «практически невозможно».
Эту ситуацию можно наглядно представить еще следующим образом:
Определение вероятности событий не такая простая штука, как кажется. Вспомните хотя бы известную шутку: «Какова вероятность того, что я встречу на улице динозавра?» — «50 на 50!» — «Это почему?» — «Ну как почему? Либо встретишь, либо нет!» На самом деле мы понимаем, что вероятность встретить свободно разгуливающего по улице динозавра равна нулю, ибо их нет в живых, к сожалению. Или к счастью.

Мы с вами изучали когнитивные искажения, поэтому вы теперь знаете главный вывод: мы склонны преувеличивать свой контроль над определением вероятности событий (эвристика доступности, иллюзия контроля, ошибка базового процента и т. д.), то есть наше субъективное представление о вероятности сильно отличается от действительной вероятности.
А теперь вспомните пример с россиянами, Никитой и рыбалкой. В индуктивных рассуждениях мы часто имеем дело со статистикой. Помните, мы с вами рассуждали, что чем больше российских мужчин любят рыбалку, тем вероятнее, что Никита из России тоже любят рыбалку. Но давайте посмотрим на другой пример:

Из частной посылки о статистических данных мы делаем вывод обо всех россиянах — классическая индукция. Вроде звучит убедительно. Но мы же понимаем, что на самом деле 100 респондентов не могут выражать мнение всей страны. И более того, возникают резонные вопросы. Кого конкретно опрашивали? Где опрашивали? При каких условиях опрашивали?
Если индукция представляет собой процесс обобщения, то принципиально важным становится вопрос выборки, то есть предмета исследования. Давайте представим простой пример: «Моя собака постоянно кусает прохожих, поэтому все собаки опасны для окружающих». Наш эмпирический опыт позволяет понять, что это не так. Не все собаки кусаются. Но как же мы понимаем, что этого примера недостаточно? И какая же выборка будет достаточной? Сколько собак нужно привести в пример, чтобы сделать вывод, что все собаки кусают прохожих?
Также хочу обратить ваше внимание на исходную формулировку в примере. Давайте сравним посылки:

Могут, как вы понимаете, отличаться и выводы в умозаключении:

Обратили внимание на слова-уточнения? «Некоторые», «большинство», «все» — от наличия или отсутствия этих слов принципиально меняется вывод умозаключения. Если я скажу, что моя собака кусает людей, то заключение в виде «моя собака опасна для окружающих» будет корректным. Однако оно вовсе не будет доказывать, что «большинство» собак или «все» собаки опасны.
Так как же понять это мерило истинности? Сколько собак нужно привести в пример, чтобы не говорить о тенденциозности вывода? Итак, предмет исследования называется выборкой. А все те (всё то), о ком или о чем надо сделать вывод, именуются генеральной совокупностью. Все прекрасно понимают, что если мы будем брать не первые случайные объекты из генеральной совокупности или какие-то специальные объекты, то все наше заключение о генеральной совокупности будет неверным.
В этом плане очень показательным будет следующий пример. Давайте представим ситуацию: я опрашиваю посетителей бара, как они относятся к алкоголю. 100 % респондентов ответили: «Крайне позитивно». Вас ничто не смущает? Все дело в том, что я провел опрос там, где априори к алкоголю относятся хорошо, ведь это бар. Такая выборка будет называться смещенной. Как вы думаете, какие будут результаты, если точно такой же опрос я сделаю на Красной площади, или в библиотеке, или в Обществе анонимных алкоголиков?
Всем понятно, что важно, чтобы выборка проводилась среди правильного и необходимого числа людей. Основных правил корректной выборки можно сформулировать три.
Во-первых, выборка должна быть большой. Чем больше объем выборки, тем надежнее она представляет генеральную совокупность и тем более правдоподобным будет наше заключение.
Во-вторых, выборка должна быть разнообразной и, главное, репрезентативной. Если перед нами задача узнать, как все граждане страны относятся к алкоголю, тогда надо опрашивать не только людей в барах. Необходимо узнать, на какие категории делятся жители нашей необъятной страны (например, по гендеру, возрасту, профессии, уровню достатка, образованию и т. д.); понять, в каких они пропорциях представлены (кого больше: мужчин или женщин, подростков или пенсионеров), и проводить выборку точно в таких же пропорциях — то есть выборка должна репрезентировать генеральную совокупность в тех же категориях и пропорциях.
Наконец, в-третьих, она должна быть случайной. Это означает, что люди из генеральной совокупности должны быть выбраны случайным, рандомизированным способом. Это позволит нам избежать смещения выборки, предвзятости и когнитивных искажений, которым, как мы знаем, подвержены и сами исследователи (вспоминаем рассмотренное ранее когнитивное искажение «эффект ожидания наблюдателя»).








