Когда Галилей подсчитал суммарное расстояние, пройденное за некоторое время, ему открылась и тайна падения предметов на землю.
Суммарное расстояние, пройденное за 1 секунду, – 1 единица.
Суммарное расстояние, пройденное за 2 секунды, – 1 + 3 = 4 единицы.
Суммарное расстояние, пройденное за 3 секунды, – 1 + 3 + 5 = 9 единиц.
Суммарное расстояние, пройденное за 4 секунды, – 1 + 3 + 5 + 7 = 16 единиц.
Вы уже заметили паттерн? Суммарное расстояние всегда равно полному квадрату. Но какое отношение нечетные числа имеют к числам квадратным? Чтобы ответить на этот вопрос, мы можем перевести числа на язык геометрии.
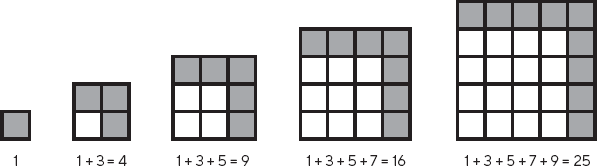
Рис. 3.1. Связь квадратных и нечетных чисел
Выкладывая очередное нечетное число по краям предыдущего квадрата, я получаю все бо́льшие и бо́льшие квадраты. Связь между квадратами и нечетными числами внезапно становится очевидной. Это – переход от арифметического рассмотрения к геометрическому – очень полезный шорткат.
Теперь Галилей смог составить формулу суммарного расстояния, которое проходит шар, падающий на землю: расстояние, пройденное через t секунд, пропорционально квадрату t. Так был открыт основополагающий квадратичный закон гравитации. В конечном итоге открытие этого уравнения дало нам возможность вычислять, где приземлится ядро, выпущенное из пушки, и предсказывать траектории планет, обращающихся вокруг Солнца.
В энный день Рождества
Тот же прием, что мы применили для демонстрации связи между нечетными числами и полными квадратами хитрым геометрическим способом, можно использовать и в качестве шортката к решению головоломки этой главы. Чтобы узнать, сколько подарков я получу от своей любви на Рождество, можно пойти длинным путем, последовательно складывая голубок и курочек. Но есть и шорткат – перевести задачу из арифметики в геометрию. Начнем с того, как геометрический подход помогает узнать число подарков, которые я получаю каждый день. Ежедневное количество подарков попросту соответствует треугольным числам, с которыми мы познакомились в главе о паттернах. Я уже рассказывал, как Гаусс разобрался с этими числами, разбив их по парам.
Но есть и другой шорткат, избавляющий от тяжелой работы: взглянуть на задачу с геометрической точки зрения. Разложим подарки треугольником, вершиной которого будет куропатка. Подсчитывать подарки, образующие треугольник, может быть непросто. А что, если составить два треугольника вместе? Тогда получится прямоугольник. Но предметы, образующие прямоугольник, подсчитать легко: нужно всего лишь умножить основание на высоту. А площадь треугольника будет половиной этого результата.
Такой геометрический шорткат к решению – это, по сути дела, тот же прием образования пар чисел, который использовал Гаусс, но слегка замаскированный. Но геометрическая точка зрения позволяет мне создать простую формулу для вычисления любого члена этой последовательности. Если мне нужно n-е треугольное число, я составляю вместе два треугольника и получаю прямоугольник размерами n × (n + 1). Теперь просто делим на 2 и находим число подарков в треугольнике: 1/2 × n × (n + 1).
Каково же суммарное количество подарков, которые я получаю по прошествии каждого дня? Вот как выглядит эта растущая сумма начиная с первого дня:
Каждое следующее число получается прибавлением очередного треугольного числа. Скажем, чтобы найти седьмое, нужно прибавить к предыдущему числу седьмое треугольное число. Поскольку седьмое треугольное число – 28, седьмой член нашей последовательности равен 56 + 28 = 84. Но нет ли еще более удобного шортката, чтобы добраться до двенадцатого члена, общего числа подарков за все рождественские праздники, без последовательного сложения треугольных чисел?
Здесь нужно еще раз перейти от чисел к геометрии. Представим себе, что все подарки приходят в коробках одинакового размера. Тогда можно составлять из полученных коробок не треугольник, а пирамиду с треугольным основанием. На ее вершине будет одна коробка, в которой находится одна куропатка на грушевом дереве. На один ярус ниже коробок уже три: одна с куропаткой и две с голубками. Каждый день приходят все новые подарки, и я добавляю их к низу пирамиды. Дает ли такой переход от чисел к геометрическим фигурам возможность понять, сколько всего коробок в пирамиде?
Как это ни удивительно, дает. Если из двух треугольников можно сложить прямоугольник, из шести пирамид одного и того же размера можно образовать прямоугольный штабель коробок. (Чтобы это получилось, вам придется слегка сдвинуть подарки, сложенные в каждую из пирамид.) Если в пирамиде n ярусов, то размеры такой прямоугольной конструкции будут n × (n + 1) × (n + 2). Но она составлена из шести пирамид. Значит, формула количества подарков в каждой отдельной пирамиде будет такой:
1/6 × n × (n + 1) × (n + 2).
Сколько же всего подарков я получу от своей любви к двенадцатому дню Рождества? Подставим в формулу n = 12 и получим 1/6 × 12 × 13 × 14 = 364. То есть по подарку на каждый день года, не считая одного!
[41]
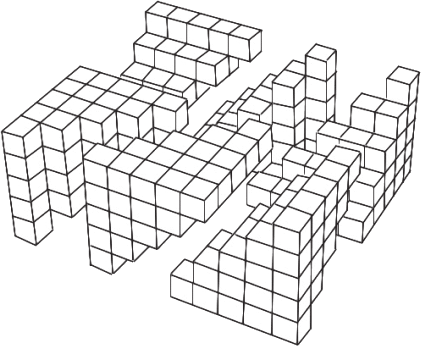
Рис. 3.2. Шесть пирамид составляют прямоугольный параллелепипед
Словарь Декарта
Меня всегда приводило в восторг то, как на картинке может проявиться нечто такое, чего не было видно за цифрами. Но нужно соблюдать осторожность. Иногда глаза обманывают нас. Взять, например, следующую картинку.
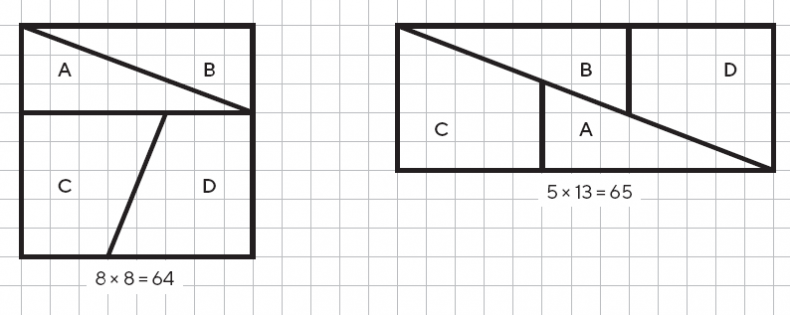
Рис. 3.3. При перестановке элементов фигуры в ней появляется лишняя клетка
Казалось бы, я просто поменял составляющие части квадрата местами так, чтобы из них получился аккуратный прямоугольник. Но погодите. Площадь квадрата равна 64 клеткам, а площадь прямоугольника – 65. Откуда же взялся этот довесок? На этой картинке трудно увидеть, что диагональ, пересекающая вторую фигуру, – не вполне прямая линия. Края составных частей не совсем прилегают друг к другу, что и приводит к появлению лишней клетки. Декарт, как известно, говорил: «Чувственное восприятие есть чувственный обман». С тех пор, как я увидел эту картинку, я, по-моему, никогда больше не мог полностью верить собственным глазам. Меня устраивают только строгие доказательства связей или паттернов на языке алгебры. Что, если с нечетными числами, которые я выкладывал по краям квадратов, тоже происходит нечто подобное этому хитрому фокусу?





