Из исследований Амиджича неясно, в самом ли деле все сводится к одной лишь генетике, или же мозг все-таки можно тренировать. Но его результаты, по-видимому, доказывают, что во время работы с максимальной эффективностью мозг использует шорткаты, расчищающие путь к решению от лишних мыслей.
10
Шорткаты невозможные
На фестивале Гластонбери я часто выступаю на сцене под названием «Астролябия». После выступления я стараюсь посетить все остальные площадки. Сможете ли вы найти для меня кратчайший маршрут, который начинается и заканчивается Астролябией и проходит через все остальные площадки, обозначенные на карте, по одному, и только одному, разу?
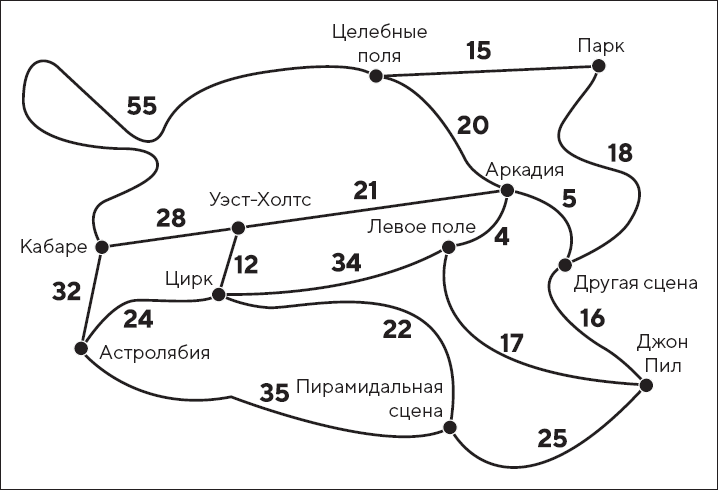
Рис. 10.1. Карта фестиваля Гластонбери
Не для всех задач существуют шорткаты. Иногда мы сталкиваемся с задачами, которые требуют физических изменений тела – например, с обучением игре на музыкальном инструменте, перенастройкой разума при помощи психотерапии, подготовкой к профессиональному спорту. Их решение требует затрат времени и сил. Но оказывается, что шорткатов могут не иметь и задачи другого рода. Сейчас математики считают, что существует огромное множество задач, получение ответов в которых невозможно без тяжелого, монотонного труда по проверке всех возможных вариантов решения.
Учитель пытается составить расписание на следующий год. Автоперевозчик прокладывает оптимальные маршруты доставки товаров для своих грузовиков. Кладовщик супермаркета ищет рациональные способы укладки коробок на полки. Футбольному болельщику не терпится узнать, сможет ли его команда победить в своей лиге. Любитель судоку хочет получить действенную стратегию решения этих дьявольских головоломок. Все они стараются найти шорткаты. Но, как ни жаль, на свете есть задачи, решению которых лучшее мышление не помогает. Даже самому Гауссу, попытайся он решить такую задачу, пришлось бы взяться за тяжкий труд перебора всех возможных сценариев. Возможно, поразительнее всего тот факт, что доказательства невозможности существования шорткатов для некоторых задач дает само искусство шортката – математика.
Классическая задача, к решению которой, по мнению математиков, не может быть шортката, называется задачей коммивояжера. В ней нужно найти кратчайший маршрут по сети городов. Ее название, по-видимому, связано с изданным в 1832 году в Германии справочником для коммивояжеров, в котором приводилась формулировка задачи и несколько примеров маршрутов по Германии и Швейцарии
[124]. Математики до сих пор не придумали для гарантированного решения этой задачи ничего умнее, чем перебор всех возможных маршрутов в поисках кратчайшего.
Беда в том, что по мере добавления новых городов число возможных маршрутов стремительно растет, и перебор всех возможных вариантов становится практически невозможным, даже на компьютере. Разве нет более быстрого способа выбрать лучшее решение? Неужели не найдется какого-нибудь очередного Эйлера или Гаусса или Ньютона, который придумал бы хитроумную стратегию определения кратчайшего маршрута? Нельзя ли, например, каждый раз просто выбирать следующим город, ближайший к тому, в котором оказался коммивояжер? Эта методика называется алгоритмом ближайшего соседа. Во многих случаях она дает весьма хорошие маршруты, всего на 25 процентов длиннее оптимального. Однако совсем не трудно построить такую сеть, в которой этот алгоритм выдает не самый короткий, а самый длинный маршрут объезда городов.
Уже были разработаны алгоритмы, гарантированно выдающие для любой сети маршруты, длина которых превышает длину оптимального маршрута не более чем на 50 процентов. Но я-то хочу получить хитрый шорткат, который позволит находить без утомительных поисков самый лучший маршрут. Эта задача настолько измучила математиков, что многие пришли к убеждению, что такого шортката просто не существует. Доказательство невозможности существования этого шортката даже стало предметом одной из семи «Задач тысячелетия», величайших нерешенных математических задач, список которых был составлен в начале XXI века
[125]. Математик, который сумеет доказать, что шортката к решению задачи коммивояжера не существует, получит в награду миллион долларов.
Что такое шорткат?
Чтобы выиграть миллионный приз, важно, собственно говоря, определить, что именно с точки зрения математики можно считать в этом контексте шорткатом. Математически различие длинного пути и шортката выражается в том, что первый приходит к решению за экспоненциальное время, а второй – всего лишь за полиномиальное. Что я имею в виду?

Рис. 10.2. Конфигурация девяти плиток, в которой узоры соседних квадратов согласуются
Эта задача сводится к нахождению алгоритмического метода, работающего не только для одной конкретной головоломки, но и для головоломок с любыми вариантами условий и размеров. Вопрос в том, как изменяется время работы алгоритма в зависимости от размера заданной ему задачи. Например, предположим, что у меня есть набор из 9 плиток, и на всех этих плитках есть разные узоры. Я хочу расположить эти плитки квадратом 3 × 3 так, чтобы узоры в смежных квадратах согласовывались друг с другом.
Сколько существует вариантов раскладки таких плиток? Для левого верхнего угла существует 9 возможностей: я могу положить туда любую из девяти плиток. У этой плитки есть 4 возможные ориентации. Всего получается 9 × 4 = 36 вариантов. Плитка, которая займет следующий квадрат, может быть любой из 8 оставшихся; у нее тоже есть 4 возможных варианта ориентации. Таким образом, суммарное число вариантов заполнения всего квадрата получается равным
где 9! обозначает произведение 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1, которое называют «9 факториал». Если компьютер может проверять по 100 миллионов вариантов в секунду, перебор всех этих возможностей займет у него чуть больше 15 минут. Не так уж и плохо. Но посмотрите, как быстро это время увеличивается с ростом числа плиток. Возьмем 16 плиток, которые нужно уложить в квадрат 4 × 4. Из рассуждений, аналогичных приведенным выше, следует, что число возможных комбинаций равно




