Ещё один пример – вши[29]. Сейчас мы осознаём, что вши – это опасные существа, разносящие опасные заболевания, но наши предки из средневековой Европы очень удивились бы такому повороту событий. Европейские аристократы наряду с прочими правилами этикета изучали также правильные по этикету способы избавления от вшей. Многие считали, что вши и вовсе оказывают положительное влияние на здоровье человека, так как у больных людей этих паразитов обнаруживали реже. Предполагали, что болезнь приходила тогда, когда человек избавлялся от вшей, но на самом же деле эти членистоногие просто очень чувствительны к температуре. Таким образом, корреляция «больше вшей – здоровее человек» никак не поможет нам установить причинно-следственную связь, а, может, даже и натолкнёт на неправильные выводы о том, что вши полезны для здоровья.
Непараметрические методы
Мы уже примерно поняли, когда нужно использовать параметрические методы. Чем же отличаются от них непараметрические? Например, вам нужно исследовать какой-то признак, который нельзя описать числами, какой-нибудь цвет или признак, который подразумевает дихотомичный ответ «да-нет». Подробнее мы остановимся на критерии Манна-Уитни и его многомерном расширении – критерии Краскела-Уоллиса. Интересно в этих методах то, что они являются ранговыми. Это означает, что каждому результату присваивается определённый «ранг». В итоге мы можем сказать о любых двух значениях только то, что одно из них больше или меньше другого, возможно, эти значения равны. Но мы никогда и ни при каких условиях не сможем сказать, на сколько именно одно значение больше или меньше другого. По факту мы всё начинаем измерять «в попугаях».
Такое упрощение даёт нам возможность вообще не заморачиваться о том, какое у нас получилось распределение, и просто наслаждаться жизнью. Мы вообще не интересуемся какими-то там средними, дисперсиями и прочей чепухой, нас интересует только то, чтобы всё как-то магически обрабатывалось. Как говорил известный английский писатель Артур Кларк: «Любая достаточно развитая технология неотличима от магии». В случае применения непараметрических методов эта фраза – наше жизненное кредо. Современные технологии позволяют нам не корпеть над вычислениями, а решать все вопросы двумя нажатиями клавиш на клавиатуре. Непараметрика на бумаге требовала бы от нас многих шагов, но мы избавились от этого, ещё и считаем «в попугаях», ну не сказка ли?
Использовать непараметрические методы необходимо довольно часто. Взгляните вновь на рис. 7: два из трёх распределений асимметричны, они далеко от нормального. Иногда такое распределение можно наблюдать даже тогда, когда, казалось бы, по всем предсказаниям и предположениям распределение должно соответствовать гауссиане. Но жизнь всегда вносит свои коррективы, поэтому повторюсь: мы не освобождены от проверки на нормальность.
Самое интересное, что далеко не факт, что непараметрические методы, применённые на нормальных выборках, покажут исследователю какой-то сущий бред. Есть такой термин, чувствительность теста. Определение этого термина интуитивно понятно: то, насколько тот или иной критерий чувствителен к выявлению различий. Забавный факт в том, что непараметрические методы будут также чувствительны и на нормальных выборках, но чувствительность параметрических методов на таких выборках будет больше. Верно и обратное, хотя параметрика показывает себя на ненормальных распределениях куда хуже.
Кто не рискует, тот не пьёт лекарства
Очень часто в медицинских исследованиях можно увидеть такие непонятные аббревиатуры, как OR и RR. После этого обычно идут какие-то непонятные числа, потом какая-то непонятная аббревиатура CI, а потом ещё какие-то числа… Что это такое и что с этим делать, как оно вписывается в наши представления о статистике?
Дело в том, что в медицине очень важно оценивать риски. Врачи делают это регулярно. Да даже если вы возьмёте в руки инструкцию к какому-то препарату, в очень многих случаях вы сможете увидеть фразу: «…если вероятная польза от лечения превышает возможный риск…» Чаще всего эту фразу можно встретить в разделе инструкции, посвящённом применению препарата беременными женщинами. Ведь некоторые лекарства могут быть опасны для плода, как мы с вами знаем на примере талидомида, поэтому существуют специальные категории, которые определяют класс опасности лекарства для плода.
Риск – это тоже своего рода вероятность. Только в данном случае, как правило, подразумевается что-то не очень хорошее, например наступление болезни или её осложнения. Как и любая другая вероятность, риск принимает значения от нуля до единицы. Под нулём понимают такой исход, когда условная болезнь ни при каких условиях не наступает. Если же риск равен единице, то болезнь наступает всегда, во всех случаях. В медицинских исследованиях оценка рисков позволяет, например, определять, насколько применение лекарств безопасно в тех или иных случаях.
Относительный риск в русскоязычной литературе обычно сокращается до ОР (но не следует путать с отношением рисков), в англоязычной литературе сокращается как RR (relative risk). Представьте, что в исследовании вы проверяете, как марсианская голубика действует на состояние ваших пациентов. Часть пациентов при этом ест марсианскую голубику, а вторая часть не ест её. В каждой из этих групп пациентов будут случаться какие-то неблагоприятные исходы, например, кто-то руку сломает, у кого-то давление скакать будет. В зависимости от того, связаны эти события с вашим исследованием или нет, вы будете их учитывать или не учитывать в конечном анализе данных. Допустим, в группе пациентов, которые ели голубику, частота неблагоприятных исходов, связанных с исследуемым вами состоянием, составила 120 пациентов из 200, а в группе пациентов, которые никакой голубики не ели, – 60 пациентов из 200. Построим такую вот табличку:
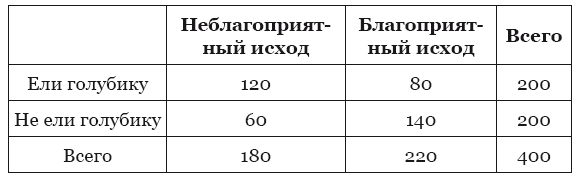
Тогда относительный риск легко найти по такой формуле:
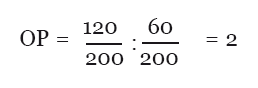
После того, как мы нашли значение относительного риска, нужно ещё найти границы так называемого 95 % доверительного интервала (в русскоязычной литературе сокращается до ДИ, а в англоязычной – до CI от confidence interval). Доверительный интервал на определённом уровне (в нашем случае – 95 %) означает, что с определённой вероятностью (в нашем случае – 95 %) значения исследуемой нами величины (в нашем случае – относительного риска) попадут в посчитанный диапазон. Доверительные интервалы рассчитываются по более сложным формулам, которые имеют отдельный вид для верхней и нижней границы интервала соответственно. Любая программа для обработки данных, однако, посчитает вам доверительный интервал в два счёта, поэтому я не буду приводить эти формулы. В нашем случае верхняя граница получится равной примерно 2.54, а нижняя – примерно 1.57.

