Вообще экстремально суровые наказания являются неприемлемыми во многих сферах деятельности. И причин здесь много. Если говорить о штрафах, то зачастую их просто невозможно собрать, даже конфисковав у коррупционера все в полном объеме. Кроме того, с моральной точки зрения чрезмерно жестокое «показательное» наказание одного из нарушителей (по сути дела ему ломается вся жизнь) также несправедливо, особенно на фоне того, что остальные коррупционеры продолжают брать взятки и наслаждаться обеспеченным существованием.
При этом сверхвысокие штрафы могут и не достигать желаемой цели устрашения. Как минимум, из-за убывающей предельной полезности денег, а также нерационального поведения агентов, встречающихся с маловероятными, хоть и очень неприятными событиями. Наконец, когда мы говорим об особенно суровых наказаниях, ставки оказываются настолько высоки, что возникает реальная опасность вовлечения в коррупционные схемы даже тех, кто проверяет проверяющих.
Какова альтернатива? Например, использование аналога описанной выше схемы наказания нарушителей, перепрыгивающих турникеты. Причем здесь чуть лучше, чем в примере с безбилетниками, обстоят дела с проблемой упорядочения. Как уже говорилось, в реальной жизни надеть на свободных граждан майки с номерами не очень просто. Кроме того, в этом есть некоторый элемент несправедливости – ведь на первый взгляд кажется, что тот, кому досталась майка с первым номером, теряет больше, чем тот, у кого номер последний. Мы же можем, например, осуществить упорядочение всех инспекторов в соответствии с предыдущими значениями xi, объявить публично данный расклад и сказать, что мы идем к «самому наглому» из тех, кто продолжит брать взятки.
1.3.3. Симметричные стратегии наказания
Что не очень хорошо в механизме наказания, изложенном в предыдущем параграфе? Необходимость строгого упорядочения всех инспекторов. Кто-то скажет, что ориентироваться на прошлые, причем недоказанные факты коррупции некорректно. А кто-то просто приведет пример, когда взятки берут все и в полном объеме, то есть xi = 1, i=1,…, n, однако нам все равно нужно будет разделить всех инспекторов на «белых» и «черных».
Таким образом, предложенный алгоритм изначально должен быть асимметричен – при абсолютно одинаковом поведении разных участников он должен приводить к разным для них исходам. Возникает вопрос: а можно ли придумать что-то более справедливое?
Приведем несколько примеров. И начнем с вопроса о том, можно ли уменьшить уровень коррупции при высоком размере взяток, например превышающем величину штрафа. На первый взгляд, ответ будет отрицательным даже при гарантированном наказании. Зачем рационалу вести себя честно, если, скажем, штраф составляет миллион, а в виде взятки можно получить полтора или хотя бы миллион сто. Однако не все так просто.
Пусть, например, взяткоемкость отраслей составляет 4/3 от величины штрафа. Однако государство обещает вообще не проверять тех инспекторов, кто берет умеренно, скажем не более 30 %. А значит, мы должны сравнить две стратегии поведения, представленные на рис. 1.10.
Первая стратегия x1 = 1 состоит в том, чтобы брать взятки по полной. Поскольку b = 4/3Т, а значит, T = 3/4b, полезность инспектора от такой стратегии составляет u1 = b – 3/4b = 0,25b. Эта величина положительна, а значит, при отсутствии альтернатив все инспекторы действительно будут нарушать закон, нести наказание и продолжать свою противозаконную деятельность. Такое часто случается при высокой выгоде от оппортунизма. Скажем, люди, высоко ценящие свое время, готовы, игнорируя камеры слежения, превышать допустимую скорость или ехать в случае пробки по выделенной полосе, лишь бы размер штрафа не превышал упущенной из-за возможного опоздания выгоды.
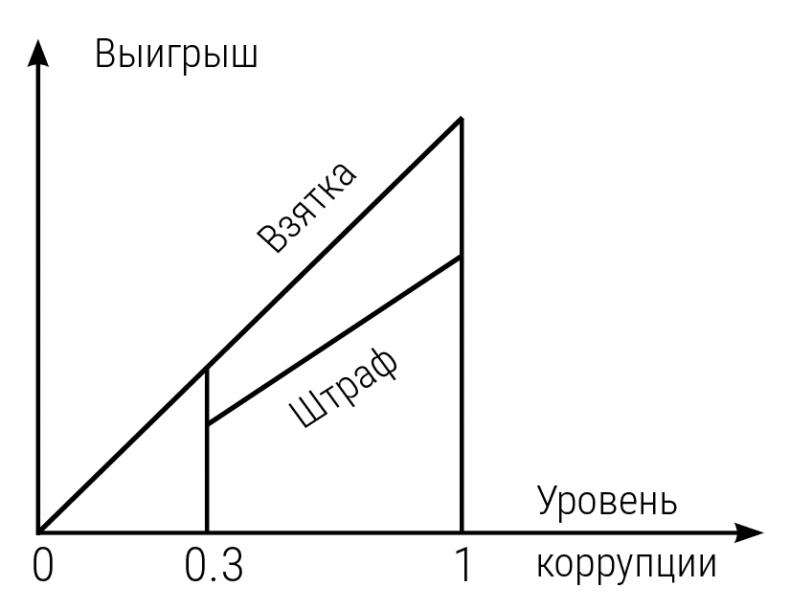
Рис. 1.10. Ступенчатое наказание
Однако в нашем случае имеется и вторая стратегия: брать взятки умеренно, перейдя на «разрешенный» уровень коррупции x2 = 0,3, честно проверяя 70 % предприятий, принося в казну соответствующую долю налогов и получив индульгенцию от государства. Полезность от такой стратегии u2 = 0,3b оказывается выше, чем от стратегии жесткого оппортунизма u1 = 0,25b, а значит, ступенчатая схема наказания действительно снижает уровень коррупции более, чем втрое.
Предыдущий пример отражал борьбу государства с единственным инспектором-коррупционером, а в новом мы вернемся к постановке с несколькими отраслями. Пусть четыре инспектора осуществляют проверку отраслей со «взяткоемкостью» b1 = 2, b2 = 3, b3 = 4 и b4 = 9 млн руб. Пусть также штраф, накладываемый на инспектора при доказательстве его вины, составляет T = 10 млн. Очевидно, что штраф превышает максимальный объем получаемых взяток, поэтому, придя с гарантированной проверкой к каждому, включая последнего, можно заставить проверяемого работать честно. Но как искоренить коррупцию полностью? Ведь последнего надо проверять с вероятностью более 90 %, а оставшихся 10 % не хватит, чтобы остановить даже первого. И тем не менее это возможно.
Схема очень проста: проверка приходит с равной вероятностью ко всем инспекторам-взяточникам, у которых xi > 0. Первый понимает, что, даже если все остальные тоже будут брать взятки, его будут проверять с вероятностью 25 %, ожидаемый штраф 0,25 ×10 = 2,5 млн превысит доход от взяток в размере 2 млн а значит, честное поведение x1 = 0 экономически оправдано. Причем это достоверно знают и остальные инспекторы.
Теперь проверяющий приходит к каждому из оставшихся инспекторов с вероятностью, не меньшей чем 1/3. Ожидаемый минимальный штраф составляет 1/3 ×10 = 3,3 млн что превышает взяточный доход второго. Вывод: второй инспектор тоже ведет себя честно, x2 = 0.
Если коррупционеров остается двое, то минимум 50-процентная вероятность проверки нарушителя закона и ожидаемый штраф в размере 0,5 × 10 = 5 млн убедят рационального третьего перейти на сторону добра: x3 = 0.
Ну а то, что оставшийся в одиночестве четвертый также не захочет нарушать закон, мы уже обсуждали.
Итак, снова коллективная ответственность привела к полному искоренению коррупции там, где, казалось бы, ресурсов для этого катастрофически не хватает. Более того, это произошло с использованием простой и понятной симметричной стратегии наказания. Никакой предварительной сортировки, тем более несправедливой сортировки (а это очень важно при применении механизмов), не осуществляется. И наконец, что также очень важно, мы получили сильное равновесие Нэша. Это означает, что выигрыш каждого участника взаимодействия нельзя увеличить не только с помощью индивидуальных, но и с помощью скоординированных действий, а значит, ситуация является устойчивой к сговору.

