Гальтон не знал подобных примеров и предполагал, что наткнулся на закон наследования, а не на закон статистики. Он полагал, что возвращение к среднему обусловлено некой причиной, и на лекции в Королевском институте наглядно проиллюстрировал свои доводы, представив публике двухуровневый квинкункс.
Пройдя первый ряд булавок, шарики попадали в наклонные пазы, которые смещали их вновь к центру доски; затем они проходили второй ряд. Гальтон торжественно показал, что эти пазы полностью компенсируют тенденцию нормального распределения расползаться вширь. В этом случае колоколообразная кривая распределения вероятностей оставалась одной и той же ширины от поколения к поколению.
Таким образом, постулировал Гальтон, возвращение к среднему — это физический процесс, с помощью которого природа обеспечивает одинаковое распределение роста (или интеллекта) в каждом последующем поколении. «Процесс регрессии сотрудничает с общим законом отклонения», — сообщил он своей аудитории. Ученый сравнил его с законом Гука, описывающим тенденцию пружины возвращаться к равновесной длине.
Не забываем, какой был год на дворе. В 1877 году Гальтон искал причинное объяснение и полагал, что регрессия к среднему — это каузальный процесс, подобный закону физики. Он ошибался, но был в этом не одинок. Многие повторяют эту ошибку по сей день. Например, бейсбольные эксперты почти всегда пытаются объяснить «проседание» чемпиона на втором году рассуждениями о причинах. «Он зазнался и расслабился», — сетуют они, или: «Другие игроки сумели найти его слабости и воспользоваться ими». Это может быть правдой, но на деле такой феномен не нуждается в объяснении причин. Чтобы оно произошло, обычно достаточно просто закона случая.
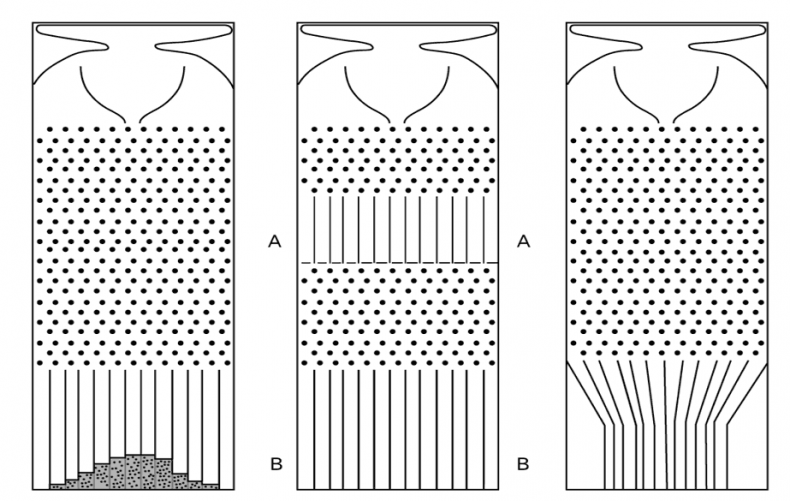
Рис. 8. Устройство, с помощью которого Фрэнсис Гальтон продемонстрировал аналогию наследования роста: а — когда через устройство вроде пинбола пропускают большое количество шариков, то в результате случайных отскакиваний они накапливаются на дне устройства, образуя колоколообразную кривую; б — при двух проходах через устройство, соответствующих двум поколениям, кривая распределения становится шире; в-чтобы упредить эту тенденцию, Гальтон придумал желобки, возвращающие шарики к центру во «втором поколении». Этими желобками Гальтон каузально объясняет явление возвращения к среднему [источник: Гальтон Ф. Естественная наследственность (1889)]
Современная статистика объясняет это явление совсем просто. В книге «Думай медленно, решай быстро» Даниэль Канеман делает вывод: «Успех — это талант плюс удача. Большой успех — это чуть больше таланта и намного больше удачи». Новичок года талантливее в бейсболе, чем большинство, но ему, скорее всего, еще и очень повезло. В следующем году ему повезет меньше и его баллы окажутся не столь впечатляющими.
К 1899 году Гальтон это понял и в процессе постижения, разочарованный, но одновременно и восхищенный открываю-щимся, предпринял первый значительный шаг к отделению статистического от причинного. Его рассуждения несколько туманны, но их стоит попытаться понять — ведь это первый, пока робкий лепет только что родившейся статистики.
Гальтон стал собирать разнообразные, так называемые антропометрические данные: рост, длину предплечья, длину и ширину головы и т. п. Он заметил, что если два размерных признака, например рост и длину предплечья, расположить на оси координат, то их сочетание проявляет все ту же регрессию к среднему. У самых высоких людей более длинные руки, чем в среднем, но длина их рук не настолько больше среднего, насколько рост. При этом очевидно, что рост не является причиной длины руки или, наоборот, в лучшем случае и то и другое имеют общую наследственную компоненту. Гальтон стал использовать новый термин для таких пар признаков: рост и длина предплечья со-отнесены, находятся в ко-реляции, ко-релируют. Со временем он перешел к более привычному нам написанию: «корреляция», «коррелируют».
Чуть позже он обнаружил еще более неожиданный факт: при сравнении поколений неважно, движемся ли мы по ходу времени или назад в прошлое. Это значит, что отцы относительно сыновей тоже проявляют возвращение к среднему. Отец сына, который выше ростом, чем популяция в среднем, оказывается почти всегда тоже выше среднего роста, но ниже, чем его сын (рис. 9). Заметив это, Гальтон был вынужден отказаться от попыток найти каузальное объяснение явлению регрессии к среднему, потому что рост сына никоим образом не может определять рост отца.
На первый взгляд, это наблюдение парадоксально. «Постойте! — скажете вы. — Значит, у более длинных отцов более короткие сыновья, а у более длинных сыновей более короткие отцы? Как эти два утверждения могут быть верны одновременно? Не может же сын быть одновременно выше и ниже своего отца».
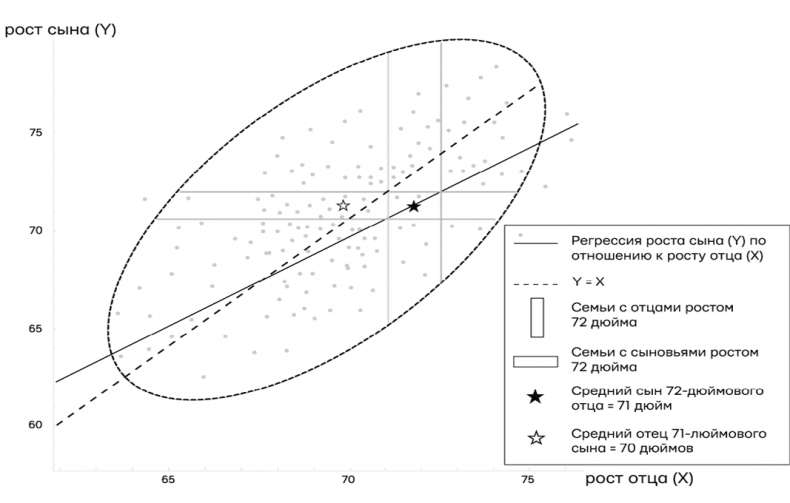
Рис. 9. Точечный график показывает набор данных о росте. Каждая точка представляет рост отца (по оси Х) и сына (по оси Y). Пунктирная линия совпадает с большой осью эллипса, а сплошная линия (ее называют линией регрессии) соединяет крайнюю левую и крайнюю правую точки эллипса. Разница между ними отражает возвращение к среднему. Например, черная звездочка показывает, что у отцов ростом 72 дюйма сыновья в среднем имеют рост 71 дюйм (т. е. средний рост у всех, чьи данные представлены точками в вертикальной полосе, — 71 дюйм). Горизонтальная полоса и белая звездочка показывают, что такое же падение роста возникает в непричинном направлении (назад во времени) (источник: график Маян Харел при участии Кристофера Баучера)
Ответ заключается в том, что мы говорим не об индивидуальных отцах и сыновьях, а о двух популяциях — отцовской и сыновней. Допустим, мы отобрали отцов, чей рост ровно 6 футов. Это больше среднего, поэтому средний рост их сыновей будет тоже выше среднего, но ближе к среднему, допустим, 5 футов и 11 дюймов. Однако множество пар, в которых рост отца равен 6 футам, не совпадает с множеством пар, в которых рост сына — 5 футов 11 дюймам. В первом множестве рост всех отцов равен 6 футам по условию задачи, а вот во втором окажется несколько отцов с ростом больше 6 футов и много отцов ниже 6 футов. Их средний рост будет ниже, чем 5 футов 11 дюймов, и таким образом регрессия к среднему снова обнаружит себя.
Другой способ наглядно изобразить регрессию — построить диаграмму, называемую точечным графиком (см. рис. 9). Каждая пара из отца и сына на нем представлена точкой, при этом ее положение по оси X определяется ростом отца, а по оси Y — ростом сына. Таким образом, отец и сын, оба ростом 5 футов 9 дюймов (или 69 дюймов), вместе окажутся на графике точкой с координатами (69; 69) прямо по центру точечного графика. Отец ростом 6 футов (или 72 дюйма) и сын ростом 5 футов 11 дюймов (71 дюйм) попадут в точку (72; 71) в северо-западной части нашей диаграммы. Обратите внимание, что облако полученных точек приближается по форме к эллипсу — факт, принципиальный для анализа Гальтона и характерный для нормального распределения для двух признаков.




