Сейчас мы увидим, что принцип коллайдера работает совершенно противоположно цепочке или вилке, если мы ограничим значение переменной в середине. Если А и С независимы с самого начала, ограничение по В сделает их зависимыми. Например, если мы посмотрим только на известных актеров и актрис (другими словами, мы наблюдаем переменную известность =1), то мы увидим негативную корреляцию между талантом и красотой: обнаружив, что актер или актриса не обладает красотой, мы укрепляемся в убеждении, что он или она отличается талантом.
Эту негативную корреляцию порой называют ошибкой коллайдера или эффектом достаточного объяснения. Для простоты представим, что для статуса звезды не нужны ни талант, ни красота — достаточно чего-то одного. Тогда, если актер А особенно хорош, это «достаточно объясняет» его успех и ему не нужно быть красивее среднего человека. В свою очередь, если актер В особенно плох, то единственный способ объяснить его успех — привлекательная внешность, т. е. с учетом результата известность = 1 талант и красота связаны обратно, даже если они не связаны между собой у людей в целом. Но и в более реалистичной ситуации, где успех — сложная функция, зависящая от красоты и таланта, эффект достаточного объяснения все же присутствует. Однако этот образец несколько апокрифичен, потому что красоту и талант трудно измерить объективно; тем не менее ошибка коллайдера вполне реальна и в этой книге мы увидим множество тому примеров.
Эти три связки — цепи, вилки и коллайдеры — подобны замочным скважинам в двери, разделяющей первый и второй уровни Лестницы Причинности. Заглянув в них, мы можем увидеть секреты причинного процесса, который породил наблюдаемые нами данные. Каждая символизирует определенный принцип причинно-следственной связи и оставляет след в виде зависимости и независимости данных друг от друга при определенных условиях. В публичных лекциях я часто называю их дарами богов, поскольку они позволяют тестировать причинно-следственную модель, открывать новые модели, оценивать эффекты интервенции и многое другое. Тем не менее, взятые в отдельности, они позволяют лишь мельком взглянуть на ситуацию. Нам нужен ключ, который полностью откроет дверь и позволит выйти на второй уровень. Этот ключ, о котором мы узнаем из главы 7, включает все три связки и называется d-разделением. Его концепция позволяет нам увидеть, какого рода зависимости можно ожидать в данных при разных шаблонах и путях в модели причинно-следственных связей. Такая фундаментальная связь между причинами и вероятностями составляет основной вклад байесовских сетей в науку о причинном выводе.
Где мой чемодан? От Ахена до Занзибара
Пока я сделал акцент только на одном аспекте байесовских сетей, а именно на диаграмме и стрелках, которые в идеале ведут от причины к следствию. В самом деле, эта диаграмма — двигатель байесовской сети. Но для любого двигателя требуется топливо. В данном случае это таблица условных вероятностей.
По-другому это можно выразить так: диаграмма описывает отношение вероятностей в качественном виде, но если нужны количественные ответы, то необходимы и количественные вводные. В байесовской сети нужно определить условную вероятность каждого узла с учетом его «родителей» (вспомним, что «родительские узлы» ведут к «дочерним»). Это прямые вероятности, P (подтверждение | гипотеза).
В случае когда А — корневой узел и на него не указывают стрелки, надо просто определить априорную вероятность для каждого состояния А. В нашей второй сети болезнь (D) → обследование (T) D — корневой узел. Таким образом, мы определили априорную вероятность того, что пациентка больна (1/700 в нашем примере), и того, что она не больна (699/700 в нашем примере).
Описывая A как корневой узел, мы на самом деле не подразумеваем, что у A нет предшествующих причин. Вряд ли какая-то переменная имеет право на такой статус. На самом деле мы имеем в виду, что любые предыдущие причины A могут быть адекватно обобщены в априорной вероятности P (A) того, что A верно. Так, в случае с болезнью и обследованием семейный анамнез может быть причиной заболевания. Но до тех пор, пока мы уверены, что семейный анамнез не повлияет на переменную обследование (как только мы узнаем статус болезни), нет необходимости представлять ее как узел на графике. Однако, если существует причина заболевания, которая также напрямую влияет на обследование, то эта причина должна быть явно представлена на диаграмме.
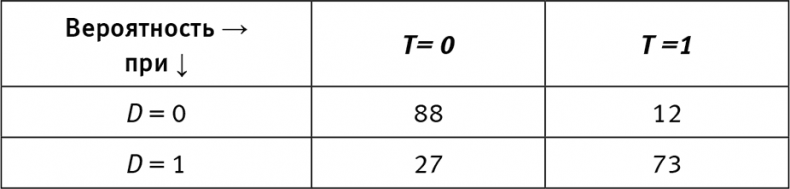
В случае если у A есть родитель, она должна «послушать» его, прежде чем определиться с собственным состоянием. В примере с маммографией родителем обследования (T) была болезнь (D). Мы можем показать этот процесс «слушания» в таблице 2 × 2 (табл. 2). Скажем, если T «слышит», что D = 0, то в 88 % случаев T будет равно 0 (T=0), в 12 % — 1 (T = 1). Обратите внимание на то, что во второй части таблицы содержится та же информация, которую предоставил Консорциум по надзору за раком груди: доля ложноположительных результатов (правый верхний угол) — 12 %, а чувствительность — 73 %. Значения в двух оставшихся клетках дополняют сумму до 100 %.
Таблица 2. Простая таблица условной вероятности
По мере того как мы переходим к более сложным сетям, таблица условной вероятности тоже становится сложнее. Скажем, если у нас есть узел с двумя родителями, в таблице условной вероятности необходимо учитывать четыре возможных состояния обоих родителей. Давайте разберем конкретный пример, который предложили Стефан Конради и Лайонел Джофф из BayesiaLab, Inc. Это сценарий, знакомый всем путешественникам. Мы назовем его «Где мой чемодан?».
Предположим, вы только что приземлились в Занзибаре, сделав очень быструю пересадку в Ахене, и ждете, пока ваш чемодан появится на багажной карусели. Другие пассажиры уже получают багаж, но вы все ждете… ждете… и ждете… Каковы шансы на то, что ваш чемодан действительно сделал пересадку в Ахене на рейс до Занзибара? Ответ зависит, конечно, от того, сколько вы уже ждете. Если сумки только появились на ленте, возможно, стоит потерпеть и подождать еще. Но если прошло много времени, перспективы ухудшаются. Мы выразим повод для переживаний количественно, сделав диаграмму причинности (рис. 16).
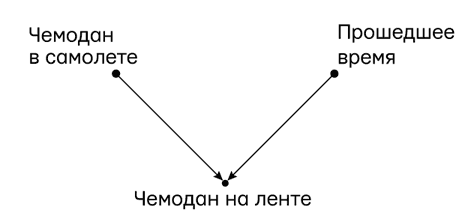
Рис. 16. Диаграмма причинности для примера с чемоданом в аэропорту
Эта диаграмма иллюстрирует интуитивную идею о том, что у появления чемодана на ленте багажной карусели есть две причины. Для начала он должен находиться в самолете — в противном случае он точно не появится на ленте. Во-вторых, присутствие чемодана на ленте становится менее вероятным с течением времени, если он вообще был на борту…

