Чтобы превратить диаграмму причинности в байесовскую сеть, надо определиться с таблицами условной вероятности. Скажем, все чемоданы в аэропорту Занзибара разгружаются в течение 10 минут. (В Занзибаре все очень эффективны!) Предположим также, что вероятность успешной пересадки вашего чемодана P (чемодан в самолете = верно) равна 50 %. (Прошу прощения, если это заденет кого-то из сотрудников ахенского аэропорта. Я всего лишь использую пример Конради и Джоффа. Сам я предположил бы более высокую вероятность — 95 %).
Настоящая рабочая лошадка этой байесовской сети — таблица условной вероятности для чемодана на ленте багажной карусели (табл. 3).
Хотя это довольно большая таблица, понять ее должно быть легко. Первые 11 строк говорят о том, что если чемодан не попал в самолет (чемодан в самолете = неверно), то, сколько бы ни прошло времени, он не окажется на ленте багажной карусели (лента = неверно), т. е. P (лента = неверно | чемодан в самолете = неверно) равна 100 %. Это объясняет 100 в первых 11 строках.
Другие 11 рядов говорят, что чемоданы выгружаются с самолета с устойчивой скоростью. Если ваш чемодан правда в самолете, есть 10 %-ная вероятность, что его выгрузят в первую минуту, 10 %-ная вероятность для второй минуты и т. д. Так, через 5 минут вероятность, что его выгрузили, будет равна 50 %, поэтому мы видим 50 P (лента = верно | чемодан в самолете = верно, время = 5). Через 10 минут все чемоданы выгружены, так что P (лента = верно | чемодан в самолете = верно, время = 10) равна 100 %. Таким образом, в последней клетке таблицы 100.
Самое интересное, что можно сделать с этой байесовской сетью, как и с большинством байесовских сетей, — решить проблему обратной вероятности. Если прошло x минут и я до сих пор не получил чемодан, какова вероятность того, что он на самолете? Правило Байеса автоматизирует это вычисление и показывает интересный момент. Через минуту эта вероятность еще равно 47 % (вспомним, что нашим изначальным предположением была вероятность 50 %). Через 5 минут вероятность снижается до 33 %. Через 10 минут, конечно же, она падает до нуля. Рис. 17 показывает, как вероятность распределяется во времени, и это можно назвать «кривой расставания с надеждой». Мне интересно, что это правда кривая: думаю, большинство людей ожидают увидеть здесь прямую линию. Вообще, отсюда следует довольно оптимистичный вывод: не отчаивайтесь слишком рано! Кривая показывает, что, когда проходит половина отведенного времени, стоит расстаться всего лишь с третью надежды.
Таблица 3. Более сложная таблица условной вероятности
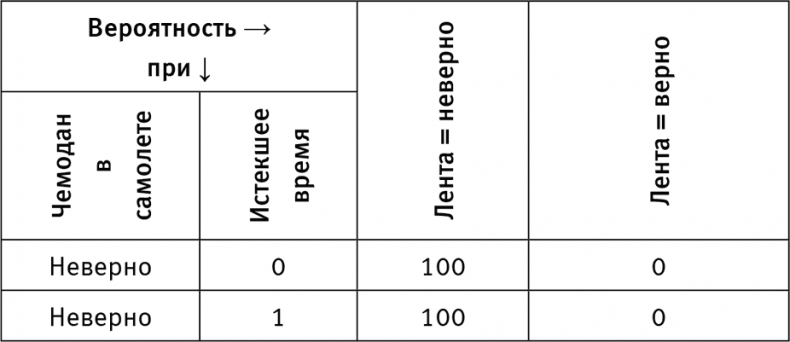
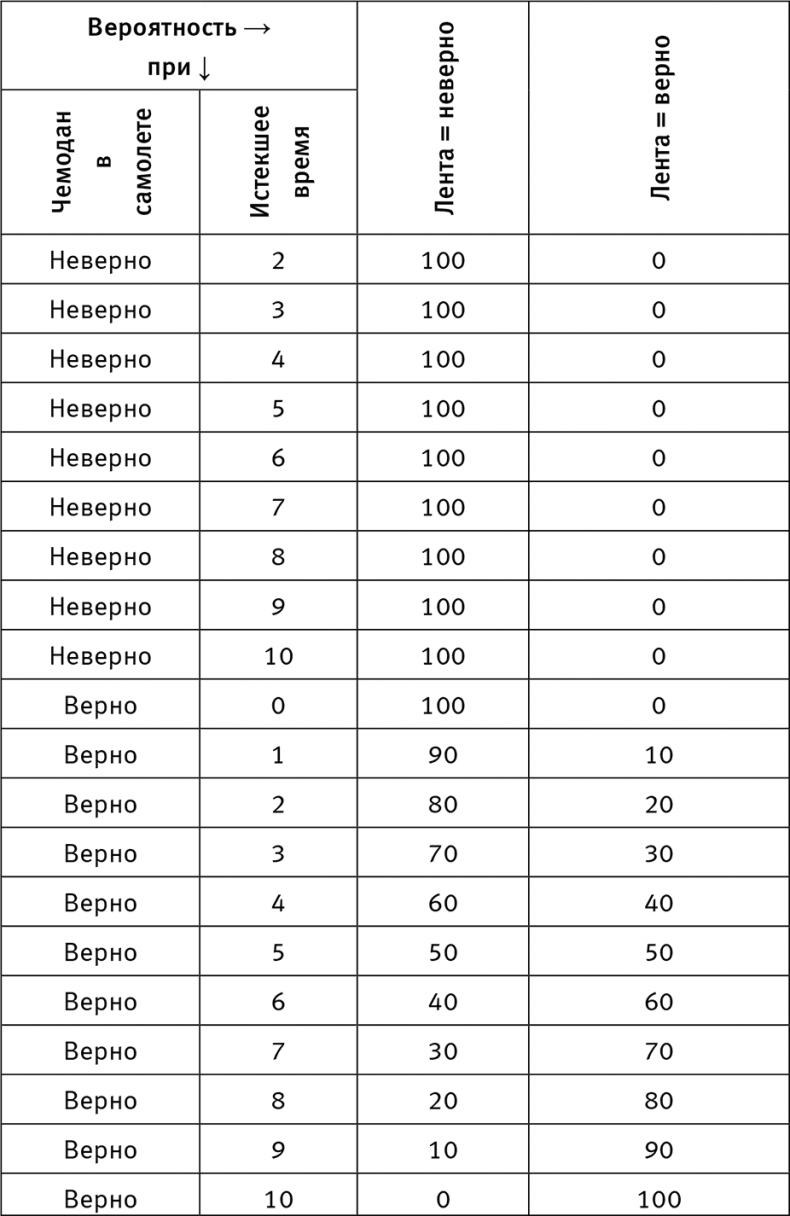
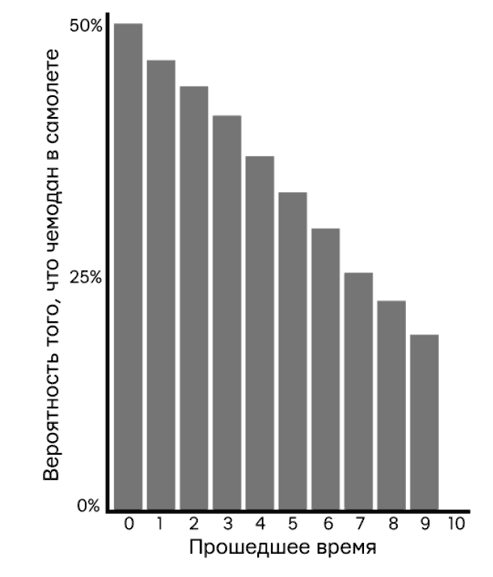
Рис. 17. Вероятность увидеть свой чемодан на ленте сначала снижается медленно, а потом быстрее (источник: график Маян Харел, информация Стефана Конради и Лайонела Джоффа)
Мы не только получили практический совет, но и поняли, что не стоит делать такие вещи в уме. Даже в крошечной сети с тремя узлами оказалось 2 ∙ 11 = 22 родительских состояния, каждое из которых влияло на состояние потомка. Конечно, для компьютера эти вычисления элементарны, но… до определенного момента. Если делать их в организованной форме, сам объем вычислений может оказаться слишком большой нагрузкой даже для самого быстрого суперкомпьютера. Если у узла десять родителей, у каждого из которого два состояния, в таблице условной вероятности будет больше тысячи рядов. А если у каждого из 10 родителей 10 состояний, то в таблице будет 10 миллиардов рядов! По этой причине необходимо отсеять связи в сети, чтобы остались только самые важные и чтобы сеть была разреженной. Одним из технических достижений в развитии байесовских сетей стало выявление способов, которые позволяют использовать эту разреженность для сокращения времени вычислений.
Байесовские сети в реальной жизни
Сейчас байесовские сети — зрелая технология и готовое программное обеспечение для них можно купить у нескольких компаний. Байесовские сети также встроены во многие «умные» устройства. Чтобы дать вам представление о том, как они используются на практике, давайте вернемся к программе Bonaparte для сравнения ДНК, с которой мы начали эту главу.
В Нидерландском институте судебной экспертизы эту программу используют каждый день, в основном расследуя дела о пропавших без вести, уголовные преступления и иммиграционные вопросы (желающие переехать в Нидерланды в статусе беженца должны доказать, что у них есть 15 родственников, живущих в стране). Однако байесовские сети продемонстрировали самый впечатляющий результат после катастрофы, такой как крушение рейса MH17 «Малайзия эйрлайнс».
Почти никого из жертв авиакатастрофы не удалось идентифицировать, сравнив ДНК с места катастрофы с ДНК из центральной базы данных. Следующим логичным шагом было взять у родственников образцы ДНК и искать частичные совпадения с ДНК жертв. Традиционные (небайесовские) методы позволяют это сделать, и они сыграли важнейшую роль в раскрытии нескольких давних преступлений в Нидерландах, США и других странах. Например, простая формула под названием «индекс отцовства» или «индекс сиблинга» помогает оценить вероятность того, что не идентифицированная ДНК принадлежит сыну или брату человека, чья ДНК есть у экспертов.
Однако эти индексы дают ограниченный результат, потому что они работают только для одного типа родства и только для близких родственников. Идея Bonaparte состоит в том, чтобы можно было использовать данные о ДНК более дальних родственников или от нескольких родственников сразу. Bonaparte делает это, преобразовывая родословную семьи в байесовскую сеть (рис. 18).
На рис. 19 мы видим, как Bonaparte переводит один небольшой кусочек родословной в (причинную) байесовскую сеть. Главная проблема состоит в том, что генотип индивида, который определяет генетическая экспертиза, содержит элементы, полученные и от отца, и от матери, но мы не можем определить их происхождение. Таким образом, два этих элемента (которые называются «аллели») необходимо рассматривать как скрытые, неизмеримые переменные в байесовской сети. Часть задачи состоит в том, чтобы вывести вероятность причины (ген голубых глаз был унаследован от отца) из имеющейся информации (например, есть гены голубых глаз и черных глаз; у кузенов со стороны отца голубые глаза, но у кузенов со стороны матери черные глаза).
Это задача на определение обратной вероятности, для чего и было изобретено правило Байеса.
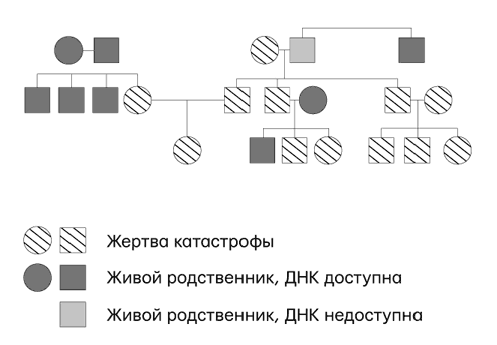
Рис. 18. Фактическая родословная семьи с несколькими погибшими в авиакатастрофе рейса MH17 «Малайзия эйрлайнс» (источник: данные предоставлены Виллемом Бургерсом)

