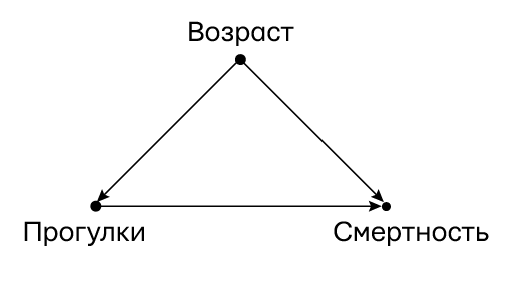
Рис. 22. Каузальная диаграмма для примера с ходьбой
Отдавая должное Эбботу и его группе, надо сказать, что у них действительно были причины для такой осторожности. Это было первое исследование на указанную тему, и выборка была относительно невелика и однородна. Тем не менее такая осторожность отражает более общую точку зрения, выходящую за пределы гомогенности и размеров выборки. Исследователей приучили полагать, что работы, основанные на наблюдениях (такие, где испытуемые сами выбирают экспериментальные воздействия), не могут выявить действие каузальных факторов. Я считаю, что эта осторожность избыточна. Зачем еще прилагать усилия и вводить поправки по всем конфаундерам, если не для того, чтобы избавиться от ложной части связи и таким образом лучше понять каузальную часть? Вместо того чтобы говорить: «Конечно, мы не можем», как поступили они, нам следует провозгласить, что, разумеется, мы в состоянии кое-что сказать о намеренной интервенции. Если мы верим, что команда Эббота идентифицировала все важные конфаундеры, мы должны верить и тому, что намеренные занятия ходьбой непременно продлевают жизнь (по крайней мере, в случае японских мужчин).
Это прогностическое умозаключение, основанное на предположении, что никакие другие конфаундеры не играют сколько-нибудь значительной роли в выявленных отношениях переменных, — очень важная информация. Она точно сообщает потенциальному спортсмену, какого рода неопределенность остается, если принять это утверждение по номиналу. Она говорит, что остаточная неопределенность не выше, чем вероятность, что существуют дополнительные осложнители, которые не были приняты во внимание. Она также ценна тем, что определяет направление будущих исследований, которые должны сосредоточиться на этих других факторах (если они существуют), а не на тех, которые были нейтрализованы в данной работе. Короче говоря, знать набор допущений, которые стоят за данным выводом, не менее важно, чем пытаться обойти эти допущения при помощи РКИ, с которым как мы сейчас увидим, много своих сложностей.
Искусное дознание природы: почему РКИ работают
Как я уже говорил выше, есть одно обстоятельство, при котором ученые перестают избегать говорить о причинности: это происходит тогда, когда им удается провести рандомизированное контролируемое исследование. Вы можете прочитать об этом в Википедии или в тысяче других мест: «РКИ часто считается золотым стандартом клинических испытаний». За это нам надо благодарить Р. Э. Фишера, так что весьма любопытно, что человек, очень близкий к нему, пишет о том, какие умозаключения привели его к этому. Цитата большая, но ее стоит привести полностью:
«Искусство и практика научного эксперимента целиком состоят в искусном допросе Природы. Наблюдение снабдило ученого видением Природы в некотором ее аспекте, у которого есть все недостатки добровольного показания. Он желает проверить верность своей интерпретации этого показания, для чего задает вопросы, нацеленные на установление причинно-следственных отношений. Его вопросы, в форме экспериментальных действий, в необходимой степени детальны, и он должен полагаться на последовательность Природы, делая общие выводы из ее ответа в отдельном случае или предсказывая исход на основании подобных операций в других случаях. Его цель — вывести обоснованные заключения определенной точности и уровня обобщения из полученных им показаний.
Природа, однако, ведет себя далеко не последовательно, ее ответы переменчивы, жеманны, двусмысленны. Она отвечает на вопрос в той форме, в которой он поставлен перед ней в эксперименте, а не в той, которая в голове у экспериментатора; она не собирается переводить ответы на понятный ему язык; ничем не делится даром; и она помешана на точности. Поэтому экспериментатор, который хочет, например, сравнить два удобрения, потратит время впустую, если, разделив свое поле на две равные части, удобрит одну одним, а вторую другим, затем засеет и сравнит собранный урожай между двумя половинами. Вопрос его задан так: какова разница между урожаем с участка А при условиях 1 и урожаем с участка Б при условиях 2? Он не спросил сначала, будет ли участок А давать урожай, одинаковый с участком Б при одинаковых условиях, и он не сможет отделить влияние свойств участка от влияния экспериментальных условий, поскольку Природа, в соответствии с запросом, записала не только вклады каждого из двух различных удобрений в урожай, но и вклады, определяемые различиями между участками в плодородии почв, структуре, водоотведении, расположении, микрофлоре и сотнями других переменных».
Автор этого отрывка — Джоан Фишер Бокс, дочь Рональда Фишера, он взят из написанной ею биографии ее прославленного отца. Хотя сама она не посвятила себя статистике, она явно очень глубоко понимает главный вызов, с которым статистики сталкиваются. Она недвусмысленно утверждает, что вопросы, которые они задают, «нацелены на установление причинно-следственных связей». А то, что стоит у них поперек дороги, — это конфаундеры, хотя она и не употребляет этот термин. Они хотят узнать влияние удобрения (тогда говорили «унавоживания»), т. е. ожидаемую урожайность при применении одного удобрения в сравнении с урожайностью при применении альтернативы. Природа, однако, говорит им о влиянии удобрения в смеси (помните термин «вмешивающаяся переменная»?) со следствиями множества других причин.
Мне нравится образ, который Фишер Бокс предложила в процитированном отрывке: природа словно джинн из сказки, который отвечает точно на тот вопрос, который мы ему реально задали, а не на тот, который хотели бы задать. Но нам приходится верить (а Фишер Бокс, очевидно, верит), что ответ на тот вопрос, который мы хотим задать, действительно существует в природе. Наши эксперименты — это довольно неряшливый способ получить этот ответ, но они ни в коем случае не определяют его. Если мы точно следуем ее аналогии, то do (X = x) должно быть сначала, потому что это свойство природы, представляющее искомый ответ: как повлияет на урожай применение первого удобрения на всем поле? Только затем идет рандомизация, потому что это присущий человеку способ получить ответ на данный вопрос. Можно сравнить ее с датчиком термометра, который представляет собой способ измерения температуры, но не саму температуру.
В молодые годы, работая на опытной станции в Ротамстеде, Фишер обычно применял очень сложный, систематический подход, для того чтобы отделить влияние удобрения от других переменных. Он делил свои поля на сетку из небольших участков и тщательно планировал исследование так, чтобы каждое удобрение было испробовано с каждым опытным видом растений и типом почвы (рис. 23). Он проделывал это с целью получить уникальные образцы для сравнения их между собой; в реальности он никогда не смог бы предугадать все конфаундеры, способные определять плодородие данного участка. Достаточно умный джинн сможет победить любую самую совершенную схему структурирования поля.
Примерно в 1923 или 1924 году Фишер догадался, что единственный дизайн исследования, неподвластный «джинну», — это случайность. Представим, что мы ставим этот же самый эксперимент 100 раз на поле с неизвестным распределением плодородия почвы. Каждый раз вы назначаете то или иное удобрение для того или иного участка поля случайным образом. Иногда вам очень не везет, и вы назначаете удобрение 1 как раз на те участки, которые сами по себе наименее плодородны. В другой раз, наоборот, оно случайно попадает на плодородные участки. Но если вы свободно и случайно тасуете части поля при всякой следующей итерации эксперимента, можно гарантировать, что эффект везения или невезения нивелируется. В этом случае удобрение 1 будет назначено на определенной общей выборке участков поля, репрезентативно представляющей поле в целом. Это как раз то, что и нужно для контролируемого опыта. Поскольку распределение плодородности по полю остается одним и тем же во всех итерациях эксперимента — «джинн» не может его изменить, — он оказывается вынужден ответить (ну чаще всего!) на тот каузальный вопрос, который вы ему задали.

