С нашей современной точки зрения в эпоху, когда рандомизированные опыты — это золотой стандарт, все вышесказанное может казаться очевидным. Но в то время сама идея случайности в схеме эксперимента привела коллег Фишера на статистическом поприще в откровенный ужас. Неприязнь усиливало, вероятно, и то, что Фишер буквально вынимал карты из тасованной колоды, назначая то или иное удобрение для определенных участков поля. Подчинить науку причудам шанса — каково!
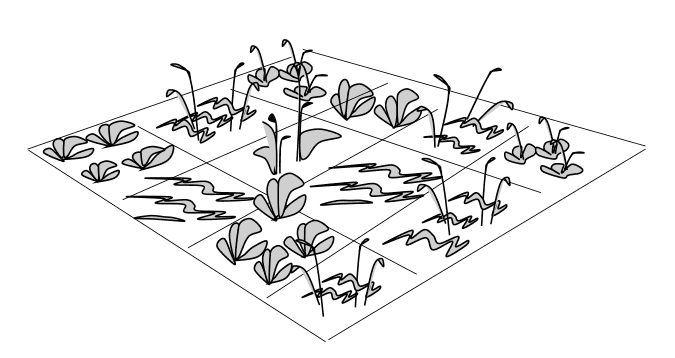
Рис. 23. Одна из множества придуманных инноваций Р. Э. Фишера — схема исследования «латинский квадрат», согласно которой один участок, засаженный данным типом растений, появляется в каждой строке (тип удобрения) и в каждом столбце (тип почвы). Подобные схемы все еще используются на практике, но Фишер затем убедительно показал, что рандомизированная схема еще более эффективна.
Однако Фишер хорошо понимал, что не очень точный ответ на правильный вопрос гораздо лучше, чем очень точный ответ на неверный вопрос. Если задавать «джинну» неправильные вопросы, вам никогда не выяснить у него то, что вы хотите знать. Если же вы ставите вопрос правильно, отдельные неверные ответы — гораздо меньшая проблема. Вы можете оценить, насколько эти ответы неточны, потому что неточность образуется в результате процедуры рандомизации (которая известна и понятна), а вовсе не из-за характеристик почвы на участках (которые неизвестны).
Таким образом рандомизация дает нам два преимущества. Первое — она элиминирует системную ошибку (благодаря ей мы правильно задаем вопрос природе). Во-вторых, она позволяет исследователю оценить неточность ответа. Тем не менее, согласно историку Стивену Стиглеру, Фишер ратовал за рандомизацию преимущественно из-за второго момента. В подсчете неточности, или, статистическим языком, ошибки, ему не было равных в мире, он разработал для этого множество новых математических процедур. При этом его понимание вмешивающихся переменных и их устранения было чисто интуитивным, поскольку ему недоставало математической символики, для того чтобы адекватно передать то, что он искал.
Теперь, через 90 лет, мы можем воспользоваться оператором do, чтобы ответить на вопросы, которые Фишер хотел, но не мог задать. Давайте взглянем с каузальной точки зрения, каким образом рандомизация позволяет нам задать «джинну» правильный вопрос.
Начнем, как обычно, с каузальной диаграммы. Модель 1, показанная на рис. 24, показывает, как урожайность каждого участка определяется при нормальных условиях, когда фермер решает, как удобрять тот или иной участок, руководствуясь предвзятостью или прихотью. Вопрос, который он хочет задать джинну по имени Природа, таков: «Какова будет урожайность при однородном применении удобрения 1 (в сравнении с удобрением 2) на всем поле?». Или в терминах оператора do: каково P (урожай do (удобрение = 1))?
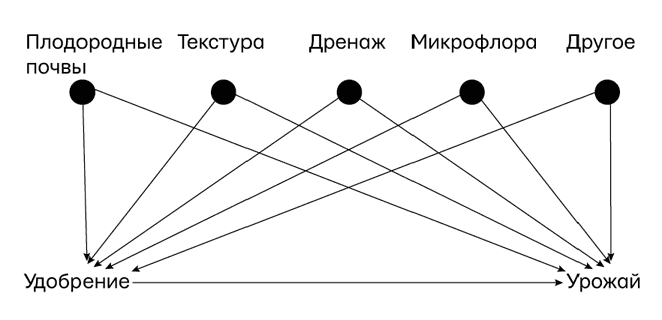
Рис. 24. Модель 1: неправильно контролируемое исследование
Если фермер ставит эксперимент наивно, например применяя удобрение 1 на верхней части поля, а удобрение 2 на нижней, то в качестве вмешивающейся переменной у него, вероятно, окажется дренированность. Если в один год он применит удобрение 1, а на другой — удобрение 2, то вмешивающейся переменной окажется погода. В любом случае сравнение окажется необъективным.
То, что хотел бы знать фермер, описывается моделью 2, когда все участки получают одно и то же удобрение (рис. 25). Как объяснялось в главе 1, действие оператора do — стереть все стрелки, идущие к «удобрению», и придать этой переменной определенное значение, положим удобрение = 1.
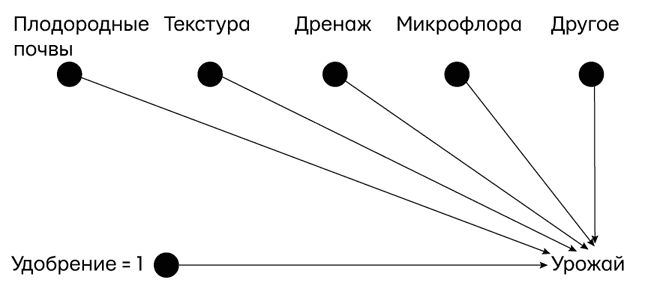
Рис. 25. То, что мы хотели бы знать
Наконец, давайте посмотрим, как все будет выглядеть после применения рандомизации. Теперь на некоторых участках поля будет do (удобрение = 1), а на других do (удобрение = 2), но выбор — какое воздействие будет оказано и на какой участок — окажется случайным. Эта ситуация описывается моделью 3 на рис. 26, в которой значение переменной удобрение назначается рандомизирующим устройством, например колодой карт, как у Фишера.
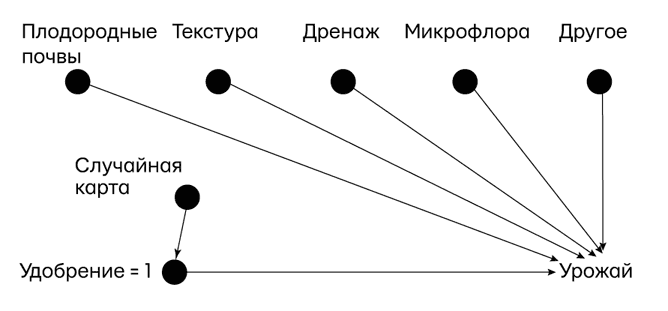
Рис. 26. Модель 3: ситуация, симулированная рандомизированным контролируемым опытом
Обратите внимание, что все стрелки, направленные к переменной удобрение, теперь исчезли, отражая предположение, что фермер в своем выборе удобрения на участке руководствуется только выпавшими картами. Не менее важно и то, что от переменной карта к переменной урожайность нет стрелки, потому что растения не знают, что на карте (в случае растений это надежное допущение, но если рандомизированный опыт ставится на людях, об этом стоит подумать). Таким образом, модель 3 описывает ситуацию, в которой отношения между переменными удобрение и урожайность не осложнены (т. е. у них нет никакой общей причины). Это значит, что в ситуации на рис. 26 наблюдение удобрение = 1 — это то же самое, что и интервенция удобрение = 1.
Это подводит нас к ключевому выводу: рандомизация — это способ симулировать модель 2. Она убирает все имевшиеся конфаундеры, не внося новых. В этом источник ее силы: в ней нет ничего таинственного или мистического. Это всего лишь, как выразилась Джоан Фишер Бокс, «искусный допрос Природы». Эксперимент, однако, утратил бы свою объективность, если бы экспериментатор назначал бы удобрения по своему выбору или если бы растения на участке «знали», какая карта им выпала. Вот почему клинические исследования с участием людей приходится организовывать с большим вниманием к тому, чтобы информация о выборе была сокрыта от глаз как испытуемых, так и экспериментаторов (эта процедура называется двойным слепым исследованием).
Я добавлю к этому второй итоговый вывод: есть и другие способы симулировать ситуацию модели 2. Один из них состоит в том, чтобы выявить все конфаундеры, измерить их и внести по ним поправки. Однако рандомизация обладает одним огромным преимуществом: она обрывает все входящие каузальные связи к исследуемой переменной, включая те, о которых мы не знаем, и те, которые не в состоянии измерить (см. факторы «Другое» на рис. 24–26).
Напротив, в нерандомизированном эксперименте исследователь должен полагаться на свое знание предмета. Если он уверен, что его каузальная модель учитывает достаточное число факторов, устраняющих вмешивающиеся переменные, и по ним собрано достаточно данных, тогда возможно оценить влияние удобрения на урожайность объективно. Однако всегда сохраняется опасность, что какая-то вмешивающаяся переменная осталась неучтенной и оценка окажется неточной.






