Игра 1
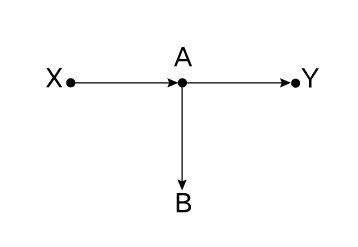
Эта — совсем простая! К X не идет ни одной стрелки, следовательно, черных ходов нет. Нам не нужно вводить никаких поправок.
Тем не менее некоторые исследователи сочтут B конфаундером. Оно связано с X по цепочке X → A → B. Оно связано с Y у особей, у которых X = 0, потому что имеется открытый путь B ← A → Y, не проходящий через Х. И при этом B не находится на каузальном пути X → A → Y. Таким образом, оно проходит трехступенчатое «классическое эпидемиологическое» определение конфаундера, но не соответствует критерию черного хода и поправки, введенные по нему, чреваты неприятностями.
Игра 2
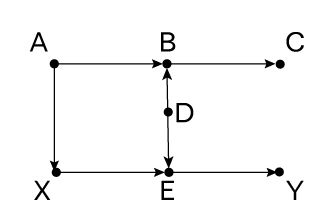
В этом примере следует рассматривать A, B, C и D как «доэкспериментальные» переменные (экспериментальное воздействие, как всегда, обозначено X). Теперь имеется один черный ход X ← A → B ← D → E → Y. Этот путь уже блокирован коллайдером в B, поэтому нам опять не нужно вводить никаких поправок. Многие статистики стали бы выравнивать выборки по B или C, думая, что в этом нет вреда, поскольку они случаются до опыта. Один известный статистик еще совсем недавно писал: «Избегание введения поправок по некоторым наблюдаемым ковариантам… это ненаучная кустарщина». Он неправ: поправки по B или C — плохая идея, потому что они откроют некаузальный путь и создадут конфаундеры между X и Y. Обратите внимание, что в этом случае мы можем снова закрыть этот путь, корректируя по A или D. Этот образец показывает, что доступны различные стратегии устранения конфаундеров. Одни исследователи пойдут легким путем и не будут вводить никаких поправок; более традиционный подход предполагает корректировку по С и D. Оба варианта верны и приведут к одному и тому же результату (если модель верна, а выборка достаточно велика).
Игра 3
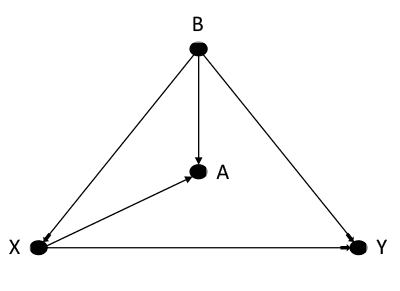
В играх 1 и 2 вам не нужно было ничего делать, но теперь придется. Имеется один черный ход от X к Y, X → B ← Y, который можно заблокировать, только вводя поправки по B. Если B невозможно наблюдать непосредственно, тогда оценить влияние X на Y невозможно без проведения рандомизированного контролируемого исследования. Некоторые (на самом деле почти все) статистики в этой ситуации будут выравнивать по A, как по опосредованной переменной для не поддающейся наблюдению переменной B, но это только частично устраняет смещение от конфаундера и вносит новое смещение от схождения.
Игра 4
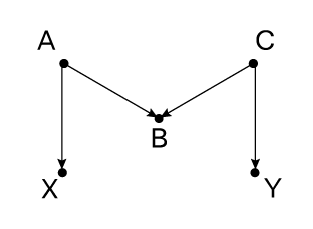
Эта игра представляет новый для нас тип смещения оценки — М-тип (названный так по форме данного графа). Снова у нас только один черный ход, уже заблокированный коллайдером в B. Таким образом, нам снова не нужно вводить поправки. Тем не менее все статистики до 1986 года и многие даже сегодня посчитали бы B конфаундером. B ассоциировано с X (посредством X ← A → B) и с Y через путь, который не проходит через X (B → C ← Y). Оно не лежит на каузальном пути и не является нисходящим по отношению к чему-либо на каузальном пути, потому что от X к Y каузального пути нет. Таким образом, B проходит традиционный трехступенчатый тест на конфаундеры.
M-тип смещения оценки показывает пальцем, что неверно в традиционном подходе. Неверно называть такую переменную, как B, конфаундером только потому, что она ассоциирована сразу и с X, и с Y. Повторяем, между X и Y нет вмешивающихся переменных, если мы не вводим поправки по B. B становится осложнителем только тогда, когда мы корректируем данные по нему!
Когда в 90-х годах ХХ века я начал показывать эту диаграмму статистикам, некоторые из них смеялись и говорили, что на практике вероятность столкнуться с такой схемой ничтожно мала. Я не согласен! Так, использование ремней безопасности в автомобиле (B) не влияет каузально ни на курение (X), ни на рак легких (Y), это просто показатель отношения индивида к соблюдению общественных норм (A) и мер безопасности и охраны здоровья (C). Образ жизни, вытекающий из этого отношения, может влиять на подверженность заболеваниям легких (Y). На практике соблюдение использования ремней безопасности оказалось скоррелировано и с X, и с Y. В исследовании 2006 года этот фактор значился одним из первых в списке переменных, по которым предполагалось вводить поправки. Если принять приведенную выше модель, то введение поправок только по B будет ошибочно.
Обратите внимание, что вводить поправки по B совершенно нормально, если при этом корректировать результаты также по A или C. Корректировка открывает трубу коллайдеру B, точке схождения, но дополнительная корректировка по A или C закрывает ее снова. К сожалению, в примере с ремнями безопасности и курением A и C — переменные, связанные с отношением людей к определенным вопросам, и получить данные по ним крайне сложно. А если переменная ненаблюдаема, по ней невозможно внести поправку.
Игра 5
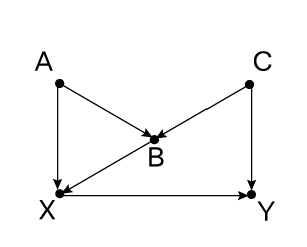
Игра 5 — почти то же самое, что и игра 4, но с небольшим дополнительным вывертом. Теперь требуется закрыть второй черный ход X → B → C ← Y. Если мы блокируем этот путь, вводя поправки по B, у нас открывается M-образный путь X → A ← B → C ← Y. Чтобы закрыть этот путь, нам придется вводить поправки также по A или C. Однако обратите внимание, что мы не сможем обойтись поправками только по C, это закроет путь X → B → C ← Y, но не затронет второй.
Игры 1–3 взяты из статьи 1993 года под названием «В поисках более ясного определения конфаундеров», написанной Кларис Вайнберг, заместителем начальника Национальных институтов здравоохранения. Она вышла в переходный период между 1986 и 1995 годами, когда статья Гренланда и Робинса уже была доступна, но о каузальных диаграммах еще не было широко известно. Поэтому Вайнберг была вынуждена немало потрудиться, арифметически доказывая взаимозаменяемость в каждом из приведенных примеров. Хотя для передачи обсуждаемых сценариев она и использовала графику, логика диаграмм для различения конфаундеров и переменных, устраняющих осложнения, не применялась. Кроме нее я не знаю никого, кому бы это удалось. Позже, в 2012 году, она стала соавтором дополненной версии статьи, где те же примеры проанализированы с помощью каузальных диаграмм и подтверждено, что все ее выводы 1993 года верны.







