Кто был прав? А кто неправ? И почему задача вызвала такие страсти? Все три вопроса заслуживают внимательного рассмотрения. Давайте сначала посмотрим, как справилась с задачей вос Савант. Ее решение поражает простотой и выглядит убедительнее, чем все, что я видел в многочисленных учебниках. Она составила список из трех возможных вариантов для расположения дверей и коз, а также внесла соответствующие результаты для стратегий «Поменять» и «Не менять» (табл. 5). Во всех трех случаях предполагается, что сначала вы выбрали дверь 1. Поскольку все перечисленные возможности (изначально) равновероятны, шанс на выигрыш, если сменить дверь, составляет две трети, а если не менять — одну треть. Обратите внимание, что в таблице вос Савант явно не указано, какую дверь открыл ведущий. Эта информация подразумевается в колонках 4 и 5. Например, во второй строке мы учли, что ведущий должен открыть дверь 3, поэтому смена выбора приведет вас к двери 2 и выигрышу. Точно так же в первой строке открытой может быть дверь 1 или дверь 2, но в столбце 4 правильно указано, что, сменив выбор, вы проиграете в любом случае. Даже сегодня многие люди, которые впервые видят эту головоломку, не могут поверить в результат. Почему? Какой интуитивный нерв им защемили?
Таблица 5. Три сочетания дверей и коз в «Заключим сделку» показывают, что вариант сменить дверь вдвое привлекательнее
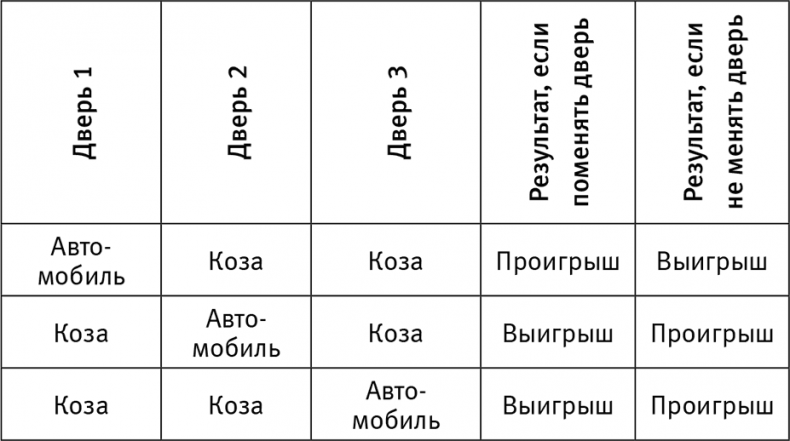
Вероятно, на это есть 10 тысяч разных причин, по одной на каждого читателя, но я считаю самым убедительным аргументом такой: нам кажется, что решение вос Савант принуждает верить в телепатию. Если я должен изменить выбор независимо от того, какую дверь предпочел в начале, значит, продюсеры каким-то образом читают мои мысли. А иначе как им удастся расположить машину таким образом, чтобы она с большей вероятностью оказалась за дверью, которую я не выбрал?
Ключевой элемент для разрешения этого парадокса состоит в том, что необходимо принять в расчет не только данные (т. е. факт, что ведущий открыл конкретную дверь), но и процесс генерации данных, другими словами, правила игры. Они сообщают кое-что об информации, которую можно было бы получить, только мы этого не сделали. Неудивительно, что именно статистикам было так трудно понять решение головоломки. Они привыкли к тому, что Р. Э. Фишер в 1922 году назвал сокращением данных, и традиционно игнорируют процесс их генерации.
Для начала давайте немного поменяем правила игры и посмотрим, как это повлияет на наш выбор. Представьте альтернативную игру с ведущим по имени Хонти Молл. Он открывает одну из дверей, на которую вы не показывали, но его выбор абсолютно случаен, т. е. он может открыть и ту дверь, за которой находится автомобиль. Такая вот незадача!
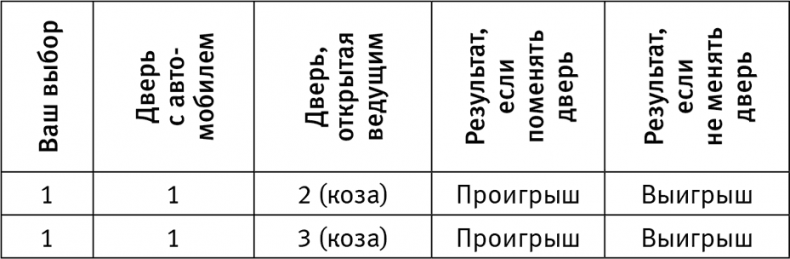
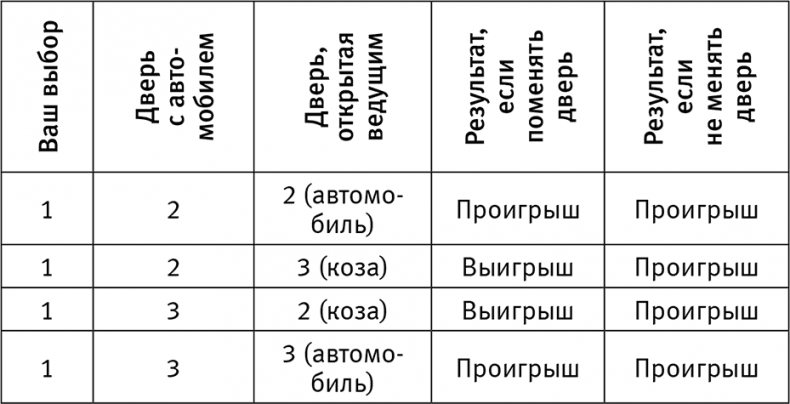
Чтобы рассмотреть этот вариант, составим таблицу, похожую на предыдущую, и примем во внимание факт, что расположение машины (три возможности) и выбор двери, которые сделает Хонти Молл (две возможности) — два случайных и независимых обстоятельства. Таким образом, в таблице должно быть шесть строк, каждая из которых равновероятна, потому что обстоятельства независимы друг от друга (табл. 6).
Что же произойдет, если Хонти Молл откроет дверь и за ней окажется коза? Так у нас появится важная информация: вероятно, мы находимся на второй или четвертой строке таблицы. Сосредоточившись только на второй и четвертой строках, мы увидим, что отказ от изначального выбора больше не дает нам никакого преимущества — в любом случае вероятность выигрыша будет равна одной второй. Таким образом, применительно к шоу Хонти Молла критики Мэрилин вос Савант были бы правы! Однако в двух этих случаях мы имеем дело с разными данными. Урок здесь довольно прост: то, как мы получаем информацию, не менее важно, чем сама информация.
Таблица 6. Варианты в программе с Хонти Моллом
Давайте воспользуемся нашим любимым приемом и нарисуем диаграмму причинности, которая сразу же покажет, чем отличаются две телеигры, реальная и воображаемая. Во-первых, на рис. 32 показана диаграмма для настоящей игры «Заключим сделку», где Монти Холл должен открыть дверь, за которой нет машины. Отсутствие стрелки между вашей дверью и местонахождением автомобиля означает, что ваш выбор двери и выбор продюсера, где поставить машину, не зависят друг от друга. Так мы явно исключаем возможность чтения мыслей со стороны продюсеров (или с вашей стороны!). Но еще важнее две стрелки, присутствующие на диаграмме. Они показывают, что на открывшуюся дверь повлиял и ваш выбор, и выбор продюсеров. Дело в том, что Монти Холл должен открыть дверь, отличную и от «вашей двери», и от «местонахождения автомобиля» — ему необходимо принять в расчет оба фактора.
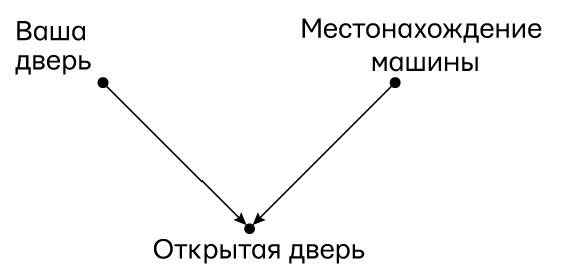
Рис. 32. Диаграмма причинности для шоу Монти Холла
Как следует из рис. 32, открытая дверь — это коллайдер. Как только у нас появляются данные об этой переменной, все наши вероятности становятся зависимыми от полученной информации. Но, если учитывать только коллайдер, создается ложная зависимость между его родителями. Зависимость подкрепляется вероятностями: если вы выбрали дверь 1, то вероятность присутствия автомобиля за дверью 2 будет в два раза выше, чем шанс найти его за дверью 1; если вы выбрали дверь 2, то в два раза выше вероятность его присутствия за дверью 1.
Это определенно странная зависимость, к которой большинство из нас не привыкло. У этой зависимости нет причины. Она не связана с физическим общением между продюсерами и нами. Она не подразумевает телепатию. Это чистый эффект байесовской обусловленности: волшебная передача информации без причинности. Наш разум восстает против такой возможности, потому что с раннего детства мы научились связывать корреляцию с причинностью. Если машина позади нас делает те же повороты, что и мы, сначала мы думаем, что она следует за нами (причинно-следственная связь!). Потом нам приходит в голову, что она просто едет в то же место (т. е. за каждым поворотом стоит общая причина). Но беспричинная корреляция противоречит здравому смыслу. Таким образом, парадокс Монти Холла подобен оптической иллюзии или фокусу: он использует наши собственные когнитивные механизмы, чтобы обмануть нас.
Почему я говорю, что, когда Монти Холл открыл дверь 3, произошла «передача информации»? Ведь вы не получили никаких подтверждений того, что поступили верно, выбрав дверь 1. Вы заранее знали, что он собирается открыть дверь, за которой спрятана коза, и это случилось. Никто не попросит вас изменить это мнение, поскольку вы стали свидетелем неизбежного. Так почему же вероятность выигрыша за дверью 2 выросла с до?






