С исторической точки зрения примечательно, что Симпсон в статье 1951 года, которая вызвала всю эту шумиху, сделал то же самое, что и я. Он представил две истории с абсолютно одинаковыми данными. В одном примере было интуитивно понятно, что агрегирование данных оказалось, как он выразился, «разумной интерпретацией»; в другом более разумным стало разделение данных. Итак, Симпсон понял, что это парадокс, а не просто инверсия. Однако он не предложил никакого решения, кроме как использовать здравый смысл. И самое важное: он не предположил, что, если история содержит дополнительную информацию, которая позволяет различить «разумное» и «неразумное», возможно, статистикам стоит учесть ее при анализе.
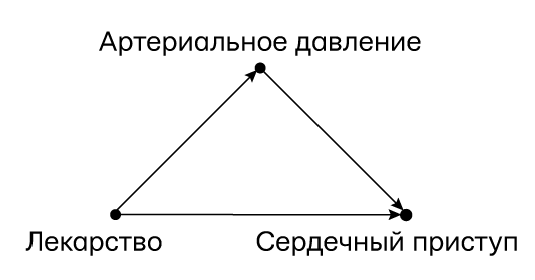
Рис. 43. Диаграмма причинности для примера с парадоксом Симпсона (второй вариант)
Деннис Линдли и Мелвин Новик рассмотрели это предположение в 1981 году, но не смогли примириться с гипотезой, что правильное решение зависит от причинной истории, а не от данных. Они признали: «Мы могли бы использовать язык причинно-следственных связей… Мы решили этого не делать и вообще не обсуждать причинность, потому что, хотя это понятие широко используется, у него как будто нет четкого определения». Так они обобщили фрустрацию пяти поколений статистиков, которые понимали, что информация о причинно-следственных связях чрезвычайно необходима, но язык для ее выражения безнадежно отсутствует. В 2009 году, за четыре года до смерти в возрасте 90 лет, Линдли признался мне, что он не написал бы приведенные выше слова, если бы моя книга была доступна в 1981 году.
Некоторые читатели моих книг и статей предположили, что правило, регулирующее агрегирование и разделение данных, основывается на временном приоритете в обработке и скрытой третьей переменной. Они утверждают, что в случае с артериальным давлением данные необходимо агрегировать, потому что измерение давления происходит после того, как пациент принимает лекарство, но в случае с полом данные нужно стратифицировать, потому что пол пациента определен заранее. Хотя это правило работает во многих случаях, его нельзя считать универсальным. Простой случай — M-тип (игра 4 в главе 4). Здесь B может предшествовать A; тем не менее мы все равно не должны ставить условие на B, потому что это нарушит критерий черного хода. Мы должны обратиться к причинно-следственной структуре рассказа, а не к временной информации.
Наконец, вы можете задаться вопросом, возможен ли парадокс Симпсона в реальном мире. Ответ будет положительным. Конечно, он встречается недостаточно часто, чтобы статистики наблюдали его ежедневно, однако он не совсем неизвестен и, вероятно, происходит чаще, чем об этом сообщают статьи в научных журналах. Вот два задокументированных случая.
Наблюдательное исследование, опубликованное в 1996 году, показало, что открытая операция по удалению камней в почках чаще завершалась успехом, чем эндоскопическая операция, которую, делали при небольших камнях. Кроме того, оно продемонстрировало, что, если камни в почках были больше, повышался и процент успеха. Но в целом для открытой операции он был ниже. Как и в нашем первом примере, выбор метода лечения зависел от состояния пациента: если камни были крупнее, открытая хирургическая операция была вероятнее, но прогноз оказывался хуже.
В исследовании заболеваний щитовидной железы, опубликованном в 1995 году, курильщики продемонстрировали более высокий коэффициент выживания (76 %) в течение 20 лет, чем некурящие участники (69 %). Но у некурящих этот показатель был выше в шести из семи возрастных групп, а в седьмой разница оказалось минимальной. Фактор возраста явно повлиял и на курение, и на выживание: средний курильщик был моложе среднего некурящего (возможно, потому что курильщики старшего возраста уже умерли). Разделив данные по возрастным группам, мы пришли к выводу, что курение отрицательно влияет на выживание.
Поскольку парадокс Симпсона настолько плохо поняли, некоторые статистики специально стараются его избежать. Слишком часто они пытаются бороться с симптомом, инверсией Симпсона, ничего не делая с болезнью — конфаундерами. Вместо того чтобы подавлять симптомы, необходимо обращать на них внимание. Парадокс Симпсона предупреждает нас о случаях, когда по крайней мере один из статистических трендов (в агрегированных данных, разделенных или в тех и других) не может отражать причинно-следственное влияние. Есть, конечно, и другие тревожные знаки. Если оценить причинно-следственный эффект в совокупности, получившаяся величина, к примеру, может оказаться выше, чем каждая аналогичная величина в каждой страте. И снова приходится повторять: этого не должно произойти, если мы должным образом учли вмешивающиеся факторы. Однако по сравнению с такими признаками инверсию Симпсона труднее игнорировать именно потому, что это разворот, качественное изменение знака. Идея вредного / вредного / полезного препарата вызовет недоверие даже у трехлетнего ребенка — и совершенно справедливо.
Парадокс Симпсона в картинках
До сего момента большая наши примеры инверсии и парадокса Симпсона в основном включали двоичные переменные: пациент либо принимал Лекарство D, либо нет, и либо переживал сердечный приступ, либо нет. Однако инверсия может возникнуть и с непрерывными переменными, и, возможно, в этом случае она будет понятнее за счет возможности ее проиллюстрировать.
Представьте исследование, в котором измеряют еженедельную физическую активность и уровень холестерина у людей разных возрастных групп. Если нанести количество часов, потраченных на физкультуру, на ось х и уровень холестерина на ось Y, как показано на рис. 44 (a), то для каждой возрастной группе наблюдается наклон вниз, и это, вероятно, означает, что физическая активность понижает уровень холестерина. С другой стороны, если использовать ту же диаграмму рассеяния, но не делить данные по возрастам, как на рисунке 44 (b), то мы увидим выраженную направленность вверх, которая говорит: чем больше люди занимаются физкультурой, тем выше их уровень холестерина. Ситуация с плохим-плохим-хорошим лекарством повторяется, только в его роли выступает Физическая активность. Кажется, что она положительно влияет на каждую возрастную группу, но вредит населению в целом.
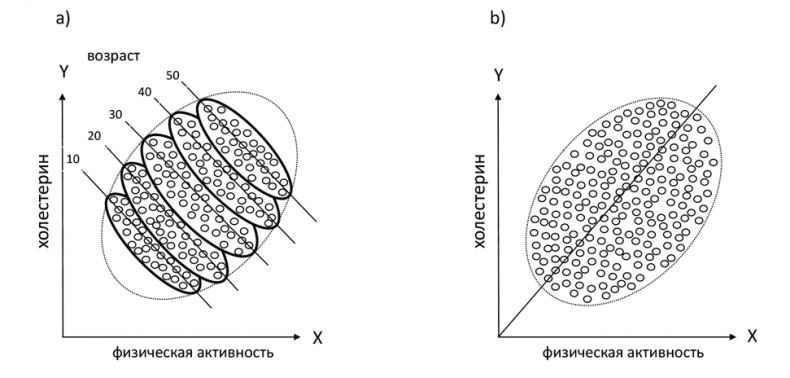
Рис 44. Парадокс Симпсона: физическая активность представляется полезной (направление вниз) в каждой возрастной группе, но вредной (направление вверх) в популяции в целом.
Чтобы решить, полезна или вредна физическая активность, мы, как всегда должны обратиться к истории, которая стоит за данными. Данные показывают, что люди старшего возраста в нашей популяции больше занимаются физическими упражнениями. Поскольку ситуация, когда Возраст служит причиной Физической активности представляется более вероятной, чем обратная, и поскольку Возраст способен оказывать каузальное воздействие на Холестерин, мы приходим к выводу, что Возраст может быть осложнителем для Физической активности и Холестерина. Значит, нужно сделать корректировку по Возрасту. Другими словами, следует посмотреть на данные, распределенные по возрастам, и мы увидим, что физические упражнения приносят пользу, независимо от возраста.

