Парадокс Лорда теперь вырисовывается с большей ясностью, поскольку запрос точно определен как воздействие рациона на прибавку веса. Первый статистик утверждает, исходя из соображений симметрии, что переход с Рациона А на Рацион В не оказал бы эффекта на прибавку веса (разница WF — WI одинаково распределена в обоих эллипсах). Второй статистик сравнивает итоговые показатели веса при Рационе A с показателями для рациона В для группы студентов, которые начали с веса W0 и приходит к выводу о том, что студенты, получающие рацион B, сильнее прибавляют в весе.
Как и раньше, данные (рис. 47 [a]) не скажут вам, кому верить, — именно к такому выводу приходят Вайнер и Браун. Однако диаграмма причинности (рис. 47 [b]) поможет разрешить этот вопрос. Между рис. 46 и рис. 47 (b) есть существенные различия. Во-первых, первичной величиной становится Рацион, а не Пол. Во-вторых, стрелка, которая изначально указывала от S к WI, теперь меняет направление: исходный вес теперь влияет на рацион, поэтому стрелка направлена от WI к D.
На этой диаграмме WI — осложнитель для D и WF, а не медиатор. Таким образом, второй статистик в этом случае будет однозначно прав. Ограничение по исходному весу необходимо, чтобы D и WF (а также D и Y) освободились от осложнителя. Первый статистик оказался бы неправ, потому что измерял бы только статистические ассоциации, а не причинно-следственные эффекты.
Подводя итог, скажем, что для нас главный урок парадокса Лорда в том, что он не более парадоксален, чем парадокс Симпсона. В одном из них ассоциация становится обратной, а в другой исчезает. И в обоих случаях диаграмма причинности подскажет, какую процедуру нужно использовать. Однако статистикам, обученным «традиционной» (т. е. не учитывающей модели) методологии и избегающим оптики причинности, представляется глубоко парадоксальным тот факт, что вывод, верный в одном случае, будет неверным в другом, при том, что данные выглядят совершенно одинаково.
Теперь, хорошо проработав коллайдеры, осложнители и опасности, которыми они грозят, мы наконец-то готовы пожать плоды нашего труда. В следующей главе мы начнем подъем по Лестнице причинности, начав со второго уровня — интервенции.
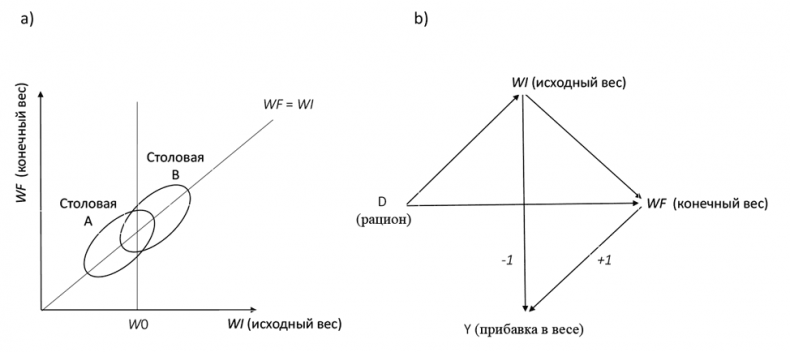
Рис 47. Обновленная версия парадокса Лорда по Вайнеру и Браун и соответствующая диаграмма причинности.
Глава 7. За пределами поправок: покорение горы интервенции
В том, у кого боязнь согрешить проявляется прежде, чем мудрость, мудрость укрепится; утратит же ее тот, у кого она проявляется прежде, чем боязнь согрешить Авот. 3:9
Раби Ханина бен Доса (I век н. э.)
В этой главе мы, наконец, храбро предпримем восхождение на второй уровень Лестницы Причинности, уровень интервенций — святой Грааль каузального мышления с древнейших времен до наших дней. Этот уровень задействован в попытках предсказать эффекты еще не испытанных действий и стратегий, от способов лечения до социальных программ, от экономической политики до личного выбора. Конфаундеры были основным препятствием, заставлявшим нас путать наблюдаемое с осуществляемым. Удалив это препятствие с помощью техники блокирования путей и критерия черного хода, мы можем картировать путь к горе Интервенции с систематической точностью. Для начинающего альпиниста самые безопасные тропы наверх — это поправки черного хода и различные родственные им техники, некоторые из них упомянуты тут в рубриках «Поправки парадного входа» и «Инструментальные переменные».
Однако не во всех случаях эти пути доступны, поэтому опытному скалолазу эта глава предоставляет универсальный инструмент картирования, так называемое do-исчисление, позволяющее исследователю обследовать и нанести на карту все пути на вершину Интервенции, как бы извилисты они ни были. Если путь зафиксирован на карте и все тросы и карабины наготове, наше восхождение на вершину обречено увенчаться успехом!
Самый простой путь: формула поправки черного хода
Для многих исследователей самый (или единственный) известный метод предсказания эффектов интервенции — поправки по конфаундерам по соответствующей формуле. Этот метод разумно использовать, когда вы уверены, что у вас есть данные по достаточному набору переменных (снимающих осложнения), чтобы заблокировать все черные ходы между интервенцией и результатом. Для этого мы должны измерить средний каузальный эффект интервенции, вначале оценив ее эффект на каждом уровне или страте, снимающих осложнение переменной. Затем мы исчисляем среднее взвешенное этих страт, где каждая из них определена в соответствии со своим распространением в популяции. Если, например, переменная, по которой вводится поправка, — это пол, мы прежде всего оцениваем каузальный эффект для мужских и женских особей отдельно, затем усредняем его, если в популяции, как чаще всего бывает, соотношение полов один к одному. Если соотношения иные, скажем особей мужского пола —, а женского —, тогда для оценки среднего каузального воздействия нужно взять соответствующим образом средние взвешенные.
Роль, которую в этой процедуре играет критерий черного хода, — это гарантия, что каузальный эффект в каждой страте переменной, снимающей осложнения, не что иное, как наблюдаемый в этой страте тренд. Таким образом, каузальный эффект можно вывести из данных по частям, страта за стратой. В отсутствие критерия черного хода у исследователей нет гарантии, что поправки оправданы.
Пример с вымышленным лекарством в главе 6 — самая простая из возможных ситуаций: одна экспериментальная переменная (лекарство D), один исход (инфаркт), один конфаундер (пол) и все три переменные бинарны. Этот пример демонстрирует, как мы получаем среднее взвешенное по условным вероятностям P (инфаркт | лекарство) в каждой из страт (пол). Но описанную выше процедуру легко модифицировать так, чтобы она годилась и для более сложных ситуаций, включая множественность конфаундеров и множественность страт.
Однако во многих случаях переменные X, Y или Z принимают численные значения: доход, или рост, или вес при рождении. Мы наблюдали это в визуальном образце с парадоксом Симпсона. Поскольку переменная способна принимать (по крайней мере, для всех практических целей) бесконечное множество возможных значений, мы не в состоянии перечислить их все в таблице, как было сделано в главе 6.
Очевидное решение — распределить численные значения переменной по конечному и удобному в использовании числу категорий. В таком решении нет ничего принципиально неправильного, однако выбор числа категорий оказывается несколько произвольным. Намного хуже, когда переменных, по которым вводятся поправки, оказывается достаточно много, число категорий растет по экспоненте, что делает исчисление по этой процедуре затруднительным; еще хуже, что во многих стратах при этом нет ни одного образца и они не могут, таким образом, дать оценку вероятности.

