Следующая легитимная трансформация знакома нам по обсуждению критерия черного хода. Мы знаем, что, если набор переменных Z блокирует все пути черного хода от X к Y, поправка по Z, do (X) эквивалентна see (X).
Следовательно, мы можем написать P (Y | do (X), Z) = P (Y | X, Z), если Z удовлетворяет критериям черного хода. Примем это как правило 2 нашей системы аксиом. Хотя это, вероятно, менее самоочевидное правило, чем правило 1, в простейших случаях это принцип общей причины Ханса Рейхенбаха, измененный таким образом, чтобы мы не путали схождения с конфаундерами. Другими словами, мы говорим, что после того, как введены поправки по достаточному набору переменных, снимающих осложнения, любая оставшаяся корреляция представляет собой истинное каузальное воздействие.
Правило 3 очень простое: оно более-менее сводится к тому, что мы можем убрать do (X) из P (Y | do (X)) в любых случаях, в которых нет каузальных путей от X к Y, т. е. P (Y | do (X)) = P (Y), если нет пути от X к Y, состоящего только из стрелок, направленных вперед. Перефразируем это правило следующим образом: если мы делаем нечто, что не влияет на Y, вероятностное распределение Y не изменяется. Помимо того, что правила 1–3 столь же самоочевидны, как и аксиомы Евклида, их можно также доказать математически, используя наше «бесстрелочное» определение do-оператора и базовые законы вероятности. Обратите внимание, что правила 1 и 2 включают условные вероятности, связанные со вспомогательными переменными Z, отличными от X и Y. Эти переменные допустимо считать контекстом, в котором исчисляется вероятность. Иногда уже само присутствие этого контекста делает преобразования законными. В правиле 3 также могут присутствовать вспомогательные переменные, но я опустил их для простоты.
Отмечу, что у каждого правила имеется простая синтаксическая интерпретация. Правило 1 разрешает добавить или удалить наблюдения. Правило 2 разрешает замену интервенции на наблюдение или наоборот. Правило 3 разрешает добавлять или удалять интервенции. Все эти разрешения действуют при определенных условиях, которые в каждом конкретном случае должны быть подтверждены каузальными диаграммами.
Теперь мы готовы продемонстрировать, как правила 1–3 позволяют нам преобразовывать одну формулу в другую до тех пор, пока (если только мы окажемся достаточно сообразительны) не получим выражение, которое нам нужно. Хотя это займет довольно много места, я думаю, что нужно все-таки наглядно показать вам, как с помощью последовательного применения правил do-исчисления получается формула парадного входа (рис. 44). Вам нет необходимости внимательно следить за каждым шагом, я показываю вам вывод формулы, чтобы вы ощутили вкус do-исчисления.
Наше путешествие начнется с целевого выражения P (Y | do (X)). Мы вводим вспомогательные переменные и трансформируем целевое выражение так, чтобы оно не содержало оператора do и совпадало, конечно, с формулой поправок парадного входа. Каждый наш шаг обосновывается каузальной диаграммой, связывающей X, Y и вспомогательные переменные, или в некоторых случаях субдиаграммами, в которых стерты стрелки, соответствующие интервенциям. Эти обоснования изображаются справа.
К do-исчислению я испытываю особые чувства. С помощью этих трех скромных правил мне удалось вывести формулу парадного входа. Это было первое каузальное воздействие, которое получилось оценить иными средствами, чем поправки по конфаундерам. Я был убежден, что без do-исчисления этого никто не сможет сделать, поэтому представил эту задачу как вызов на семинаре по статистике в Калифорнийском университете в Беркли в 1993 году и даже предложил приз в 100 долларов тому, кто ее решит. Пол Холланд, присутствовавший на семинаре, написал мне, что предложил задачу в качестве проекта своим студентам и пошлет мне решение, когда оно будет готово (коллеги рассказывали мне, что на конференции в 1995 году он таки представил длинное решение, так что, возможно, я должен ему 100 долларов, если найду его доказательство). Экономисты Джеймс Хекман и Родриго Пинто предприняли следующую попытку доказать формулу парадного входа, используя только «стандартные инструменты», в 2015 году. Им это удалось, хотя и ценой восьми страниц сложных выкладок.
В ресторане вечером накануне этой беседы я записал доказательство (очень похожее на то, что приведено на рис. 44) на салфетке для Дэвида Фридмана. Позже он написал мне, что потерял ту салфетку, не может восстановить доказательство, и спросил меня, не сохранилось ли у меня копии. На следующий день Джейми Робинс написал мне из Гарварда, сообщив, что слышал о «задаче на салфетке» от Фридмана и готов вылететь в Калифорнию ближайшим рейсом, чтобы вывести доказательство вместе со мной.
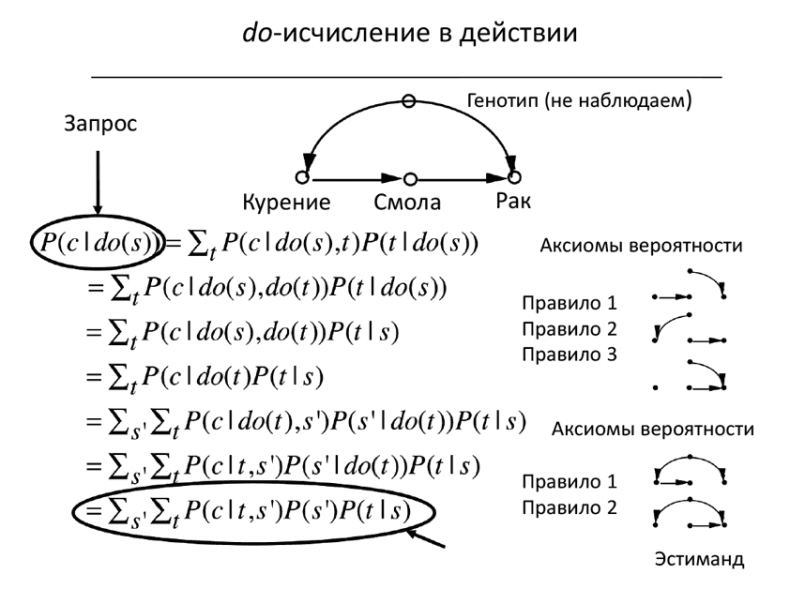
Рис. 44. Вывод формулы поправок парадного входа по правилам do-исчисления
Я был очень рад поделиться с Робинсом секретами do-исчисления и полагаю, что его поездка в Лос-Анджелес в том году сыграла ключевую роль в том, с каким энтузиазмом он воспринял каузальные диаграммы. Благодаря ему и Сандеру Гренланду эти диаграммы стали вторым языком эпидемиологов. Это объясняет, почему я так отношусь к «задаче на салфетке».
Поправка парадного входа была приятным сюрпризом и означала, что do-исчислению есть что предложить людям. Тем не менее в тот момент я еще не знал наверняка, достаточно ли всего трех правил do-исчисления. Не упустили ли мы четвертое правило, которое помогло бы нам решать задачи, неразрешимые с помощью только этих трех?
В 1994 году, когда я впервые предложил общественности do-исчисление, я выбрал эти три правила потому, что они были достаточны во всех известных мне случаях. Я не знал, выведут ли они меня как нить Ариадны из абсолютно любого лабиринта, или когда-нибудь мне попадется лабиринт такой дьявольской сложности, что выбраться из него я не смогу. Конечно, я надеялся на лучшее. Я предполагал, что в тех случаях, когда каузальное воздействие вообще возможно оценить по данному набору данных, последовательность шагов, использующих эти три правила, позволит сократить do-оператор. Но я не в состоянии был это доказать.
У такого типа задач есть множество предшественников в математике и логике. Это свойство в математической логике обычно называют функциональной полнотой. У обладающей полнотой системы аксиом есть следующее свойство: этих аксиом достаточно для выведения любого истинного утверждения данного языка. Некоторые очень хорошие системы аксиом тем не менее не обладают функциональной полнотой: таковы, например, аксиомы Филипа Давида, описывающие условную независимость в теории вероятности.
В этом современном мифе о лабиринте роль Ариадны для моего блуждающего Тезея сыграли две группы исследователей: Имин Хуан и Марко Вальторта из Университета Южной Каролины, а также мой собственный студент Илья Шпицер из Калифорнийского университета в Лос-Анджелесе. Обе группы одновременно и независимо доказали, что правил 1–3 достаточно, для того чтобы выбраться из любого лабиринта, из которого в принципе есть выход. Я не уверен в том, что весь мир, затаив дыхание, ждал доказательства функциональной полноты этих аксиом, потому что большинству исследователей в то время хватало просто критериев черного хода и парадного входа. Тем не менее обе команды получили награды в номинации лучших студенческих работ на конференции «Неопределенность в искусственном интеллекте», проходившей в 2006 году.



