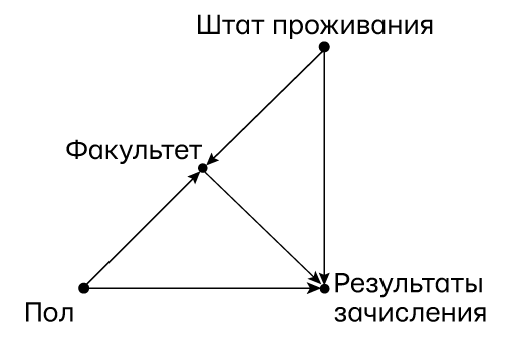
Рис. 57. Каузальная диаграмцма для парадокса зачислений в Калифорнийский университет в Беркли (версия Крускала)
Подобные аргументы показывают нам, почему концепция опосредования вызывала ранее (и до сих пор вызывает) такие подозрения. Она выглядит нестабильной и неуловимой. Результаты зачисления оказываются настроены против женщин, потом против мужчин, потом снова против женщин. В своем ответе Крускалу Бикель продолжал настаивать, что поправка по месту, где принимаются решения (факультет) чем-то отличается от поправки по критерию этого решения (штат проживания). Однако 100 %-ной уверенности, судя по всему, у него по этому поводу не было. Он спрашивает несколько беспомощно: «Здесь я вижу нестатистический вопрос: что такое перекос?» Почему знак перекоса меняется в зависимости от того, как мы его измеряем? На самом деле его идея принципиального различия между перекосом и дискриминацией была верна. Перекос, искажение — это скользкое статистическое понятие, которое может исчезнуть, если нарезать данные не вдоль, а поперек. Дискриминация, как причинностная концепция, отражает реальность, и поэтому должна оставаться неизменной вне зависимости от способа обработки данных.
Фраза, которой не хватало в словаре у них обоих, — «оставаться постоянной». Чтобы заблокировать непрямой путь от пола к результатам зачисления, мы должны зафиксировать значение переменной факультет и «покрутить» переменную пол. Когда переменная факультет принимает фиксированное значение, мы (фигурально выражаясь) не даем абитуриентам выбирать, на какой факультет подавать документы. Поскольку в статистике нет слова для этого понятия, обычно делается нечто с виду похожее: вводится поправка по переменной факультет. Именно это сделал Бикель: он стратифицировал данные по факультетам и заключил, что дискриминации нет. Эта процедура законна, когда переменные факультет и результаты зачисления не имеют осложнителей; в этом случае «видеть» и «делать» — одно и то же. Но Крускал совершенно корректно спросил: «А что, если там есть осложнитель, например штат проживания?» Он, вероятно, и не осознавал, что шел по следам Бёркс, нарисовавшей точно такую же диаграмму.
Невозможно даже передать, насколько часто эта ошибка появлялась в рассуждениях долгие годы — по опосредующей переменной вводились поправки, вместо того чтобы придать ей постоянное значение. По этой причине я называю ее Заблуждением Опосредования. Безусловно, это заблуждение безобидно, если ни опосредующая, ни итоговая переменные не осложнены. Но если осложнители присутствуют, результаты анализа могут привести к совершенно противоположным выводам, как показал численный пример Крускала. Он демонстрирует, как легко исследователь может прийти к выводу об отсутствии дискриминации там, где она есть.
Бёркс и Крускал были исключениями своего времени, признавая Заблуждение Опосредования ошибкой, хотя они и не предлагали для него верного решения. Р. Э. Фишер пал жертвой этого же заблуждения в 1936 году, и сейчас, 80 лет спустя, статистика все еще не справилась с этой проблемой. К счастью, со времен Фишера наблюдается значительный прогресс. Так, эпидемиологи знают, что необходимо следить за осложнителями на пути между опосредующей переменной и итоговой. Однако есть и те, кто отказывается от языка диаграмм (как некоторые экономисты до сих пор), они жалуются и признаются, что для них объяснить, что означает это предупреждение, — просто пытка.
Хорошо, что проблема, которую Крускал однажды назвал «возможно, принципиально неразрешимой», была решена два десятилетия назад. У меня есть странное чувство, что Крускалу это решение понравилось бы, и в своем воображении я демонстрирую ему мощь do-исчисления и контрфактивной алгоритмизации. К сожалению, он вышел на пенсию в 1990 году, как раз тогда, когда правила do-исчисления постепенно формировались, и умер в 2005 году.
Я уверен, что некоторым читателям интересно, чем в итоге закончилось дело с университетом Беркли. Отвечу: ничем. Хаммель и Бикель были убеждены, что университету не о чем беспокоиться, и, действительно, никаких судебных процессов или федеральных расследований в итоге не проводилось. Данные намекали на обратную дискриминацию, в пользу женщин, и на самом деле этому были явные свидетельства: «В большинстве случаев, в которых женщинам оказывались предпочтения, дело, похоже, обстояло таким образом, что приемные комиссии старались преодолеть многолетний недостаток женщин в их областях науки», — писал Бикель. Всего спустя три года дело об антидискриминационных мерах против другого кампуса Калифорнийского университета дошло до Верховного суда. Если бы Верховный суд отменил антидискриминационные меры, подобные «льготы для женщин» стали бы противозаконными. Однако Верховный суд поддержал их, и случай с Беркли стал исторической вехой.
Истинный мудрец оставит последнее слово не за Верховным судом, а за своей женой. Почему у моей супруги было такое сильное интуитивное убеждение, что университет в целом не может дискриминировать кого-либо, если все его факультеты действуют честно? Это теорема каузального исчисления, похожая на принцип «само собой разумеется». Этот принцип в том виде, в каком его постулировал Леонард Джимми Сэвидж, относится к общему воздействию, в то время как данная теорема верна для прямого воздействия. Само определение прямого воздействия опирается на суммирование прямых воздействий в субпопуляциях.
Коротко и ясно — честность на каждом отдельном месте составляет общую честность. Моя жена была права.
Дэйзи, котята и непрямые воздействия
До сих пор мы обсуждали понятия прямого и непрямого воздействия на смутном и интуитивном уровне, но их точного научного значения я пока не давал. Давно пора устранить это упущение. Начнем с прямого воздействия, потому что это однозначно проще, и мы сможем определить одну из его разновидностей с помощью do-исчисления (т. е. на уровне второй ступени Лестницы Причинности). Сначала мы рассмотрим простейший случай, включающий три переменные: экспериментальное воздействие X, результат Y и медиатор M. Мы получаем прямое воздействие X на Y, когда мы «крутим» X, при этом оставляя M постоянным. В контексте примера с парадоксом зачислений в Беркли, мы заставляем всех поступать на исторический факультет, или, другими словами, do (M) = 0. Мы просим абитуриентов в случайном порядке указывать в анкете свой пол как мужской (do (X) = 1) или женский (do (X) = 0) вне зависимости от их настоящего пола. Затем мы наблюдаем разницу в проценте зачисленных в обеих группах. Полученный нами результат называется контролируемым прямым воздействием или КПВ (0). При записи символами:
КПВ (0) = P (Y = 1 | do (X = 1), do (M = 0)) — P (Y = 1 | do (X = 0), do (M = 0)). (9.1)
Ноль в КПВ (0) означает, что мы сделали так, чтобы опосредующая переменная M приняла нулевое значение. Мы могли бы проделать тот же эксперимент, но заставив всех подать документы на факультет инженерии: do (M = 1). Мы обозначим полученное в результате контролируемое прямое воздействие как КПВ (1).

