Итак, если имеется более одного непрямого пути от X к Y, мы оцениваем непрямое воздействие по каждому пути как произведение всех путевых коэффициентов вдоль этого пути. Затем мы получаем суммарное непрямое воздействие, суммируя все непрямые каузальные пути. В итоге суммарное воздействие X на Y равняется сумме прямых и непрямых воздействий. Это правило суммы произведений используется с тех пор, как Сьюалл Райт изобрел путевой анализ, и, строго говоря, оно действительно следует из определения суммарного взаимодействия в терминах do-оператора.
В 1986 году Рубен Барон и Дэвид Кенни сформулировали набор принципов для обнаружения и оценки опосредования в системе уравнений. Основные принципы заключаются, во-первых, в том, что все переменные связаны линейными уравнениями, которые оцениваются путем подбора их в соответствии с данными. Во-вторых, прямые и непрямые воздействия исчисляются путем подбора двух уравнений, соответствующих данным: одного с опосредующей переменной и другого без нее. Значительное изменение коэффициентов в случае, когда вводится опосредующая переменная, считается доказательством наличия опосредования.
Простота и убедительность метода Барона — Кенни снискала ему заслуженные лавры в среде общественных наук. В 2014 году их статья занимала 33-е место сверху в списке самых цитируемых работ за всю историю. Их цитировали чаще, чем Альберта Эйнштейна, чаще, чем Зигмунда Фрейда, чаще почти любого другого ученого, которого только можно вспомнить. Их статья стоит на втором месте среди всех публикаций по психологии и психиатрии, хотя она совсем не о психологии. Она о некаузальном опосредовании.
Беспрецедентная популярность подхода Барона — Кенни, без сомнения, определяется двумя факторами. Во-первых, опосредование — очень востребованная концепция. Наше желание понять, «как действует природа» (т. е. найти M в X → M → Y), вероятно, даже сильнее, чем желание подсчитать его. Во-вторых, этот метод легко редуцируется до процедуры, по простоте подобной кулинарному рецепту, основанной на знакомых концепциях статистики, дисциплины, которая долгое время претендовала на исключительное право на объективность и эмпирическую правомерность. Поэтому почти никто не заметил случившийся при этом гигантский рывок вперед — тот факт, что каузальная величина (опосредование) была определена и оценена чисто статистическими методами.
Тем не менее первые трещины в этом возведенном из регрессий оборонительном сооружении начали появляться еще в начале 2000-х, когда практики попытались обобщить правило суммы произведений для нелинейных систем. Это правило включает два допущения: воздействия вдоль разных путей аддитивны, а путевые коэффициенты вдоль одного пути перемножаются, и оба они приводят к неверным ответам в нелинейных моделях, как мы увидим ниже.
Это заняло немало времени, но в конце концов практикующие анализ опосредования окончательно пришли в себя. В 2001 году мой покойный друг и коллега Род Макдональд писал: «Я полагаю, что лучший способ обсудить вопрос обнаружения или демонстрации модерации или медиации в регрессии — это отложить всю имеющуюся по этому поводу литературу в сторону и начать с нуля». Самые свежие публикации по опосредованию, похоже, последовали совету Макдональда: контрфактивные и графические методы в них используются более часто и последовательно, чем регрессионный подход. А в 2014 году основоположник метода Барона — Кенни Дэвид Кенни опубликовал новый раздел на своем веб-сайте под названием «Каузальный анализ опосредования». Хотя я бы пока поостерегся назвать его обращенным, Кенни явно осознает, что времена меняются и анализ опосредования вступает в новую эпоху.
Теперь давайте рассмотрим простой пример того, как наши ожидания оказываются неверными, стоит нам только выйти за границы Линейной Страны Чудес. Рассмотрим рис. 60, представляющий собой слегка измененный рис. 59, на котором кандидат на рабочее место решает принять предложение тогда и только тогда, когда обещанное жалование превосходит определенную пороговую сумму, в нашем случае 10 единиц. Предложение по зарплате определяется так, как показано на диаграмме: 7 × образование + 3 × навык. Обратите внимание, что функции, определяющие навык и зарплату, все еще предполагаются линейными, но отношение жалованья к итогу нелинейно, потому что у него есть пороговый эффект.
Давайте подсчитаем для этой модели суммарное, прямое и непрямое воздействия, ассоциированные с увеличением образования на 1 единицу. Суммарное воздействие определенно равно 1, поскольку когда образование меняется с 0 на 1, зарплата поднимается с 0 до (7 ∙ 1) + (3 ∙ 2) = 13, что больше порогового значения в 10, и таким образом итог меняется с 0 на 1.
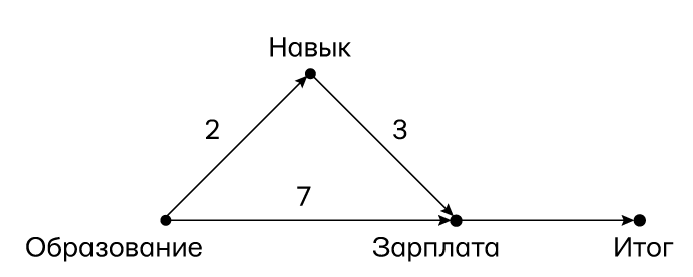
Рис. 60. Опосредование, совмещенное с пороговым эффектом
Вспомним, что натуральное непрямое воздействие — это ожидаемое изменение итога, при учете, что мы не меняем образование, но устанавливаем навык на тот уровень, который он бы принял, если мы увеличили бы образование на 1. Легко увидеть, что в этом случае зарплата увеличивается с 0 до 2 ∙ 3 = 6. Это ниже, чем пороговое значение 10, поэтому податель заявления откажется и ННВ = 0.
Что же насчет прямого воздействия? Как упоминалось выше, вопрос в том, на каком уровне нам следует удерживать опосредующую переменную. Если навык оставить на том уровне, который был до того, как мы изменили образование, тогда зарплата изменится с 0 до 7 и итог = 0. Таким образом, КПВ (0) = 0. Однако, если мы придадим навыку то значение, которое он получает после изменения образования (а именно 2), зарплата изменится с 6 до 13. Это меняет итог с 0 на 1, потому что 13 выше порогового значения для подателя заявления, и он согласится на работу. Итак, КПВ (2) = 1.
Следовательно, прямое воздействие равно 0 или 1 в зависимости от постоянного значения, которое мы придаем опосредующей переменной. В отличие от Линейной Страны Чудес выбор значения медиатора играет огромную роль, и у нас возникает дилемма. Если мы желаем сохранить аддитивный принцип, суммарное воздействие = прямое воздействие + непрямое воздействие, нам придется использовать КПВ (2) в качестве определения каузального воздействия. Но это выглядит слишком произвольно и в чем-то даже ненатурально. Если мы предполагаем изменить переменную образование и хотим узнать ее прямое воздействие, мы, скорее всего, оставим переменную навык на том уровне, который у нее был. Другими словами, интуитивно кажется более оправданным использовать в качестве прямого воздействия КПВ (0). Более того, это согласуется с натуральным прямым воздействием в этом примере. Однако тогда мы теряем аддитивность: суммарное воздействие не равно сумме прямого и непрямого воздействий.
Тем не менее — вопреки ожидаемому — несколько видоизмененная разновидность аддитивности сохраняется, не только здесь, но и вообще. Читателям, которые не испугаются небольших подсчетов, возможно, будет интересно сосчитать ННВ для возврата от X = 1 до X = 0. В этом случае зарплата падает с 13 до 7 и итог меняется с 1 на 0 (т. е. податель заявления отказывается от предложения). Подсчитанное в обратном направлении ННВ = –1.0 Восхищение вызывает тот факт, что суммарное воздействие (X = 0 → X = 1) = НПВ (X = 0 → X = 1) — ННВ (X = 1 → X = 0), или в этом случае 1 = 0 — (–1). Вы видите версию аддитивного принципа для натуральных воздействий, только в данном случае это оказывается субстрактивный (вычитательный) принцип! Я был невероятно счастлив, когда из анализа стал вырисовываться такой вариант аддитивности, несмотря на нелинейность уравнений.



