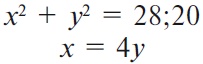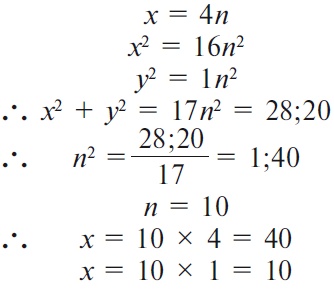Подробности хирургических операций, которые умели проводить вавилонские и ассирийские врачи, видимо, никогда не записывались писцами, и нам мало что известно об этом.
Важной частью школьной программы в школах писцов была математика, и в древневавилонский период, в который мы наилучшим образом осведомлены о школах писцов, математика Вавилонии достигла вершины своих успехов, на которую она взлетела вновь не раньше чем по прошествии еще полутора тысячелетий.
Когда только зарождалась письменность, шумеры уже разработали символы для цифр и две системы счисления: одна (десятичная) основывалась на десятке как базовой единице, а другая (шестидесятиричная) основывалась на числе 60. Эти две системы не были взаимоисключающими и обычно использовались вместе, не вызывая никакой путаницы, точно так же, как и мы (англичане. – Ред.) наряду с десятичной системой (для денег и линейных измерений) используем систему, основанную на числе 12.
К древневавилонскому периоду имелись следующие символы для обозначения чисел:

В некоторые отрезки времени и в некоторых текстах 60 изображали при помощи значка
 . Это, конечно, тот же самый значок, что и для 1, и можно было бы подумать, что это приводило к бесконечной путанице. Сравнение с нашей собственной системой цифр покажет, что это необязательно было так. Наш символ для обозначения «десяти» точно таков, как и наш символ для обозначения «один», а именно «1». Да, если мы хотим обозначить именно десять, то мы ставим после единицы ноль, но символ ноля не встречается ни в одной цифре на «-надцать». Любая из этих цифр представляет собой «1» (стоящую на определенном месте), которая является существенной частью символа для обозначения десяти, а вовсе не «10» целиком. Если бы «0» был необходимой частью символа «десять», то тогда для обозначения «пятнадцати» нам пришлось бы писать 105 (что и делают маленькие дети, прежде чем поймут нашу систему цифр). У нас в числах «пятнадцать» и «пятьдесят один» используются одни и те же символы, но в разном порядке. Использование соответствующей системы (фактически, предка нашей собственной) спасало вавилонян от путаницы, вызванной наличием значка
. Это, конечно, тот же самый значок, что и для 1, и можно было бы подумать, что это приводило к бесконечной путанице. Сравнение с нашей собственной системой цифр покажет, что это необязательно было так. Наш символ для обозначения «десяти» точно таков, как и наш символ для обозначения «один», а именно «1». Да, если мы хотим обозначить именно десять, то мы ставим после единицы ноль, но символ ноля не встречается ни в одной цифре на «-надцать». Любая из этих цифр представляет собой «1» (стоящую на определенном месте), которая является существенной частью символа для обозначения десяти, а вовсе не «10» целиком. Если бы «0» был необходимой частью символа «десять», то тогда для обозначения «пятнадцати» нам пришлось бы писать 105 (что и делают маленькие дети, прежде чем поймут нашу систему цифр). У нас в числах «пятнадцать» и «пятьдесят один» используются одни и те же символы, но в разном порядке. Использование соответствующей системы (фактически, предка нашей собственной) спасало вавилонян от путаницы, вызванной наличием значка
 для обозначения чисел «один» или «шестьдесят». Условность состояла в том, что значок
для обозначения чисел «один» или «шестьдесят». Условность состояла в том, что значок
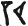 означал «шестьдесят плюс десять» (то есть семьдесят), тогда как значок
означал «шестьдесят плюс десять» (то есть семьдесят), тогда как значок
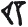 означал «десять плюс один» (то есть одиннадцать).
означал «десять плюс один» (то есть одиннадцать).
«Сто» можно было представить как «шестьдесят плюс сорок», согласно вышеизложенной системе, или написать значок
 произносимый как «ме», который является просто формой семитского слова для обозначения «ста». Имелся специальный значок для обозначения «1000» и еще один для обозначения «3600», что представляет собой 60 × 60 и является, таким образом, высшим элементом шестидесятиричной системы.
произносимый как «ме», который является просто формой семитского слова для обозначения «ста». Имелся специальный значок для обозначения «1000» и еще один для обозначения «3600», что представляет собой 60 × 60 и является, таким образом, высшим элементом шестидесятиричной системы.
Математические методы вавилонян были в основном алгебраическими, и вавилонские математики древневавилонского периода умели вычислять такие значения чисел, как квадратные и кубические корни, таблицы которых были найдены, и решать квадратные уравнения.
Далее приводится пример реальной задачи, написанной на глиняной табличке древневавилонского периода, вместе с решением. Текст гласит:
«Я сложил поверхности двух квадратов: 28;20.
<Сторона> одного квадрата равна четверти <стороны> другого квадрата.
Записываем 4 и 1.
Умножаем 4 на 4 = 16.
Умножаем 1 на 1 = 1.
Складываем 1 и 16 = 17.
Величину, обратную 17, решить нельзя. Что я должен поставить к 17 [то есть на что я должен умножить 17], чтобы получить 28;20? 1;40. Это квадрат десяти.
Увеличим 10 в четыре раза и получим 40 – <сторона> одного квадрата.
Увеличим 10 в 1 раз и получим 10 – <сторона> второго квадрата».
Вавилонское решение этой задачи гораздо проще, чем на первый взгляд говорит дословный перевод. Его можно объяснить при помощи современных алгебраических символов, хотя нужно подчеркнуть, что, хотя оно и следует, вероятно, логике мышления вавилонянина, оно не придерживается того способа, каким он его записал.
Число 28;20 записано в шестидесятиричной системе, то есть «20» представляет собой 20 раз по одному, а «28» представляет собой 28 раз по шестьдесят. «Поверхность» квадратов означает их площадь.
Давайте назовем длину стороны большего квадрата «х», длину стороны меньшего квадрата «у». Следовательно, исходя из всех данных, мы имеем уравнения:
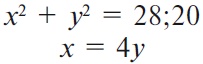
Обозначим «у» как ln. Тогда
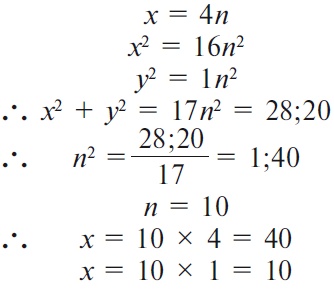
Что же касается знания геометрии, то можно сказать, что вавилонские математики знали величину «пи» с большой точностью, принимая ее за 31/8. Были найдены клинописные таблички, на которых исчислялись площади геометрических фигур.
Еще одной областью деятельности писца, имевшей отношение к математике, была астрономия. У вавилонян было две причины для того, чтобы обращать особое внимание на движение небесных тел. Одной причиной была необходимость регулировать календарь, чтобы эффективно планировать сельскохозяйственные работы. Другая же представляла собой теорию, согласно которой все события на земле являются либо отражением событий на небе, либо, по крайней мере, имеют прямое к ним отношение. Вавилоняне на самом деле думали, что могут реально видеть, что делают боги на небе. Еще в древневавилонском периоде мы находим сводки наблюдений за Венерой, охватывающие несколько лет. Затмения Солнца и Луны не могли пройти незамеченными и записывались, по крайней мере с перерывами, с очень давних времен. С середины VIII в. до н. э. (а именно, в 747 г. до н. э., по утверждению греческого астронома девять веков спустя) велись систематические записи затмений, и эти записи, ведшиеся веками, в конце концов дали возможность вычислить перемещение (или видимое перемещение) Солнца, Луны и планет относительно друг друга и в небе вообще. Однако подробности этого слишком сложны и трудны, чтобы обсуждать их здесь.




 . Это, конечно, тот же самый значок, что и для 1, и можно было бы подумать, что это приводило к бесконечной путанице. Сравнение с нашей собственной системой цифр покажет, что это необязательно было так. Наш символ для обозначения «десяти» точно таков, как и наш символ для обозначения «один», а именно «1». Да, если мы хотим обозначить именно десять, то мы ставим после единицы ноль, но символ ноля не встречается ни в одной цифре на «-надцать». Любая из этих цифр представляет собой «1» (стоящую на определенном месте), которая является существенной частью символа для обозначения десяти, а вовсе не «10» целиком. Если бы «0» был необходимой частью символа «десять», то тогда для обозначения «пятнадцати» нам пришлось бы писать 105 (что и делают маленькие дети, прежде чем поймут нашу систему цифр). У нас в числах «пятнадцать» и «пятьдесят один» используются одни и те же символы, но в разном порядке. Использование соответствующей системы (фактически, предка нашей собственной) спасало вавилонян от путаницы, вызванной наличием значка
. Это, конечно, тот же самый значок, что и для 1, и можно было бы подумать, что это приводило к бесконечной путанице. Сравнение с нашей собственной системой цифр покажет, что это необязательно было так. Наш символ для обозначения «десяти» точно таков, как и наш символ для обозначения «один», а именно «1». Да, если мы хотим обозначить именно десять, то мы ставим после единицы ноль, но символ ноля не встречается ни в одной цифре на «-надцать». Любая из этих цифр представляет собой «1» (стоящую на определенном месте), которая является существенной частью символа для обозначения десяти, а вовсе не «10» целиком. Если бы «0» был необходимой частью символа «десять», то тогда для обозначения «пятнадцати» нам пришлось бы писать 105 (что и делают маленькие дети, прежде чем поймут нашу систему цифр). У нас в числах «пятнадцать» и «пятьдесят один» используются одни и те же символы, но в разном порядке. Использование соответствующей системы (фактически, предка нашей собственной) спасало вавилонян от путаницы, вызванной наличием значка
 для обозначения чисел «один» или «шестьдесят». Условность состояла в том, что значок
для обозначения чисел «один» или «шестьдесят». Условность состояла в том, что значок
 означал «шестьдесят плюс десять» (то есть семьдесят), тогда как значок
означал «шестьдесят плюс десять» (то есть семьдесят), тогда как значок
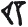 означал «десять плюс один» (то есть одиннадцать).
означал «десять плюс один» (то есть одиннадцать).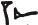 произносимый как «ме», который является просто формой семитского слова для обозначения «ста». Имелся специальный значок для обозначения «1000» и еще один для обозначения «3600», что представляет собой 60 × 60 и является, таким образом, высшим элементом шестидесятиричной системы.
произносимый как «ме», который является просто формой семитского слова для обозначения «ста». Имелся специальный значок для обозначения «1000» и еще один для обозначения «3600», что представляет собой 60 × 60 и является, таким образом, высшим элементом шестидесятиричной системы.