
Онлайн книга «Величие Вавилона. История древней цивилизации Междуречья»
Поскольку число 60 было само по себе единицей шестидесятеричной системы, оно могло обозначаться вертикальным клином, первоначально отличавшимся большим размером по сравнению с клином, обозначавшим 1, хотя различие в размере позднее исчезло. Соответственно для чисел от 60 до 99 существовали такие группы:
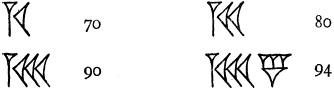
В этой системе 100 изображается так —

и действительно такое изображение часто встречается. Другим способом 100 могло изображаться (в ранний период) особенно большим кругом (имея в виду чисто десятичную систему, где 100, большой круг, считается большей степенью, чем 10, малый круг) или специальным знаком

Существуют другие модификации и
комбинации для обозначения высших числительных. Так, например, число 120 может быть представлено следующим образом:
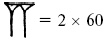
(клинья первоначально были больше, чем клин, обозначающий 1),
или (в ранний шумерский период) —
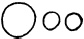
= 100 + 10 + + 10, или

= одна сотня + 20.
Числительное 1000, очень важное в десятичной системе, имело специальный знак
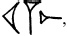
состоящий из
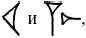
таким образом означая 10 Ч 100. В шестидесятеричной системе важным высшим числительным было 3600. Оно первоначально обозначалось очень большим кругом (также применяемым, как уже говорилось, для квадрата 10 в десятичной системе) и, наконец,
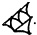
Из примеров видно, что зародыш позиционной системы счисления (системы, в которой значение каждого числового знака в записи числа зависит от его позиции относительно других знаков) уже присутствовал в числительных, используемых в Вавилонии в самый ранний период. Для читателей, у которых отношения с математикой более напряженные, отметим, что мы тоже пользуемся позиционной системой. Так, если рассмотреть числительные 15 и 51, в первом из них символ 5 означает «пять», а во втором тот же символ означает «пятьдесят». Римские числительные представляют непозиционную систему счисления: так, хотя группы VI и IV обозначают разные числительные, символ V, в каком бы положении он ни находился, означает только «пять», и
ничего более. В клинописи
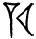
отличен от
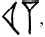
потому что в первом из них
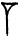
означает «шестьдесят», а в последнем – «один», так что две группы символов, частью которых является знак 3, соответственно обозначают «семьдесят» и «одиннадцать». Царь Асархаддон использовал в политике тот факт, что эти два числа отличаются в клинописи только положением двух составляющих символов. Детали см. в главе 4.
Позиционная система была развита и широко использовалась вавилонскими математиками, в начальной стадии под влиянием шкалы весов, которая встречается в экономических документах начиная с шумерского периода. Основой шумерской и вавилонской системы веса была мина: этот вес (до 1 килограмма) делился на 60 сиклей, а 60 мин составляли более крупную единицу веса – талант. Таким образом, вавилоняне были знакомы с системой X-Y-Z, в которой единицы Х составляли 60 единиц Y, а единицы Y – 60 единиц Z. Из этой концепции возникает возможность создания сложной позиционной системы счисления, основанной на шестидесятеричной системе, в которой X-Y-Z могут означать или
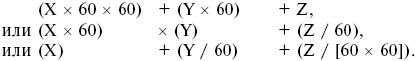
Такая система имеет два очевидных недостатка, каждый из которых проистекает из отсутствия знака зеро или символа, соответствующего точке в десятичной дроби (правильнее было бы назвать дробь «шестидесятеричной»). В нашей собственной десятичной системе число вроде 538,4 выражено точно благодаря традиции, заключающейся в том, что первая цифра слева от точки выражает единицы, вторая – десятки, третья – сотни, в то время как первая цифра справа от точки выражает десятки. Те читатели, кто с математикой на ты, надеюсь, простят мне пространные объяснения того, что для них очевидно. Однако есть читатели, которые сочтут полезным или даже удивительным упоминание о том, что вся наша десятичная система, по сути, является набором условий и обычаев, а не частью самой природы числа. В числе 358 три десятки представлены числом 3, а пять сотен – числом 5, причем их величина становится однозначной именно благодаря позиции. Неопределенность может возникнуть, если в числе нет десяток или нет единиц; в таком случае неопределенность в нашей системе ликвидируется помещением знака зеро на соответствующее место. Если соответственно нет десяток или нет единиц, чтобы представить числа 508 или 530, мы обычно не пишем 58 или 53, что может нести в себе неопределенность, и используем символы 508 и 530. (Исключение может наблюдаться при десятичном умножении или делении, когда число 53 может представлять или 5,3, или 530, причем во многих случаях ошибки не будет.)
