В руках профессионала анализ цифр состоит из множества разных тестов, а также вычисления их статистической значимости. Первичным этапом сравнения должна быть история одного и того же набора данных. Расходы текущего квартала должны сравниваться с расходами предыдущих кварталов. Нигрини называет этот принцип «Мое правило» – по модели базовых имен, предложенных программным обеспечением для новых файлов («Мой файл», «Моя таблица» и так далее). «Мое правило» позволяет избежать самой распространенной ошибки дилетантской нумерологии, предполагающей, что все числовые базы данных в точности описываются законом Бедфорда. Это ошибочное допущение. Признаки придуманных чисел, выявленные Чапанисом, тоже не обеспечивают стопроцентной защиты. По необъяснимым причинам эти методы могут оказаться применимыми или не применимыми в каждой конкретной ситуации. Проще и надежнее использовать в качестве основы прошлые распределения цифр.
В конце концов, любое мошенничество начинается в какой-то момент времени. Если Стэн из бухгалтерии начнет жульничать в следующий вторник, это изменит распределение цифр в его суммах – независимо от того, насколько настоящие данные близки к «случайным» или соответствовали кривой Бенфорда.
В качестве иллюстрации «Моего правила» Нигрини приводит эксперимент, придуманный в 2011 г. на занятиях по математике 17-летним студентом Ка Буи из немецкого города Кобленц. Класс был поделен на пять групп по четыре студента в каждой. Одним группам выдали газеты и предложили составить список из 500 чисел, встреченных в новостях. Другим группам предложили придумать 500 чисел. Смысл эксперимента в том, чтобы проверить, можно ли отличить числа, взятые из новостей, от придуманных, только по распределению составляющих их цифр.
Чтобы максимально затруднить задачу, группам, придумывавшим числа, предложили имитировать те, что могли быть найдены в газете (в противоположность случайным). В этом случае усиливалось сходство с настоящим мошенничеством, ведь преступник похож на хамелеона.
Ни один из пяти наборов данных, настоящих и поддельных, не соответствовал кривой Бенфорда, однако с первого взгляда можно было определить, что они составляют две группы. В одной наблюдались «высокие пики» – пары двух первых цифр, встречавшиеся гораздо чаще, чем ожидалось. Во второй пики были меньше, и распределение в большей степени соответствовало кривой Бенфорда. Как мы уже убедились, повторяющиеся пары цифр могут свидетельствовать о неосознанности – или о мошенничестве. Вы можете подумать, что группа с «маленькими пиками» состояла из настоящих чисел, взятых из газет. И ошибетесь.
Вспомните, что фальшивые числа придумывали группы из четырех человек. Из-за того, что разные люди неосознанно предпочитают разные цифры, вклад каждого члена группы делился на четыре. Это затруднило выявление обмана.
Реальный признак был следующим. В газетах много раз встречалось упоминание текущего года (2011) и нескольких предшествующих. Поэтому на гистограммах отмечался пик для 20 как пары первых цифр. Составители таблицы фальшивых чисел также использовали числа, обозначающие год, но в недостаточном количестве.
Тот, кто использует закон Бенфорда и признаки Чапаниса в качестве критерия, придет к выводу, что группы данных с маленькими пиками настоящие. Однако разумнее было бы проанализировать распределение цифр в числах, взятых из других газет. Это выявило бы массовое упоминание текущего года и помогло бы правильной идентификации.
Когда цифры в числах, имеющих важное значение, не соответствуют ожидаемому распределению, хороший следователь способен выяснить причину. Тем не менее, существует пара несложных, пригодных для самостоятельного применения тестов, помогающих быстро выявить подозрительные данные. На следующих нескольких страницах я продемонстрирую некоторые способы обнаружить вероятность фальсификации или манипулирования числами. Эти тесты предназначены в основном для различения реальных данных и на 100 процентов сфальсифицированных одним человеком. Столь резкий контраст вы увидите не всегда. Тем не менее, во многих случаях именно один-единственный мошенник снабжал своих жертв полностью фальшивыми данными. Эти тесты, используемые в качестве предварительной оценки, быстры и не связаны с дальнейшим анализом, а ведь вы, скорее всего, захотите его провести.
Каждое воскресенье владелица ресторана быстрого питания начинала с того, что придумывала объем продаж в долларах за предыдущую неделю. Ей нужно было отчитываться в налоговые органы. Любая цифра была фальшивой!
Совершенно случайно бухгалтер ресторана оказался одним из студентов Нигрини. Нигрини посмотрел на придуманные числа. «Ее выдали не первые цифры», – объяснил он. Ресторан быстрого питания с устойчивым бизнесом может иметь выручку, скажем, $5000 в день, с не очень большими отклонениями. Первые цифры данных не будут соответствовать распределению Бенфорда – и не должны. Подлог выдали две последние цифры. Ни одно из чисел не оканчивалось на 00. Это весьма распространенный признак, поскольку мошенники считают, что круглые числа выглядят недостаточно случайными. Кроме того, около 6,5 процента чисел оканчивались на 40 (при ожидаемой величине всего 1 процент). Использование пары 40 для двух последних цифр – неосознанная склонность владелицы ресторана.
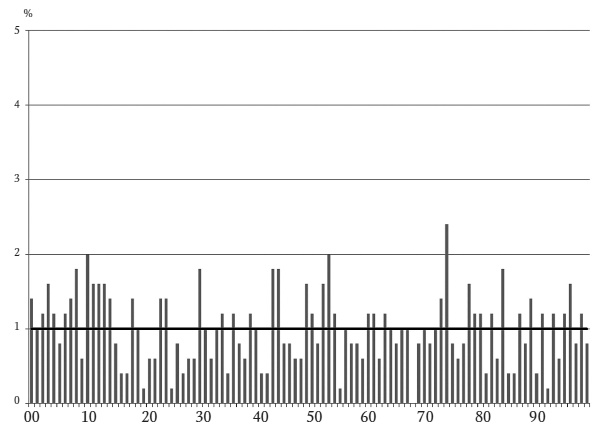
Последние две цифры: 500 случайных чисел
Когда-нибудь ресторан быстрого питания выставят на продажу, и покупатели внимательно изучат бухгалтерские документы. Возможно, для демонстрации владелица придумает новые, раздутые числа. Возникнет ли у покупателей подозрение, что вся отчетность взята с потолка?
В мелком бизнесе показатели ежедневных продаж – это сумма большого количества граф «итого» в кассовых аппаратах. Последние две цифры этих сумм обычно бывают случайными – каждая пара от 00 до 99 появляется приблизительно в 1 проценте случаев.
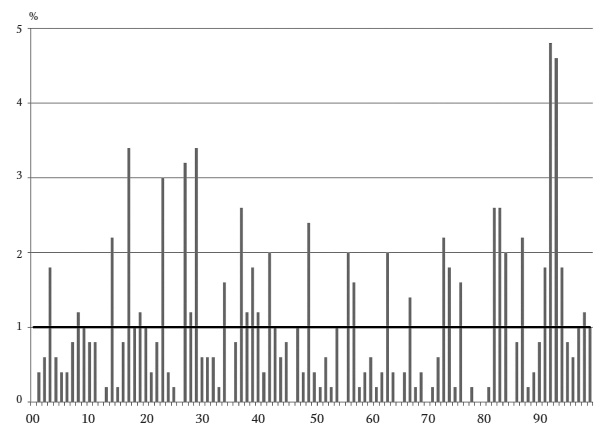
Последние две цифры: 500 придуманных чисел
Однако не во всех документах указываются суммы с точностью до цента. Иногда их округляют до долларов или даже до тысяч долларов. В таких случаях нужно использовать две крайние цифры справа.
Чтобы провести тест последних цифр, подсчитайте, сколько раз каждая из возможных пар встречается в имеющемся наборе данных. Всего таких пар 100, и поэтому потребуется составить гистограмму из 100 столбиков.
Ниже приведена гистограмма, дающая представление, как выглядят реальные данные. Она характеризует выборку из 500 случайных чисел (сгенерированных программой Excel). Число 500 достаточно репрезентативно для мелкого бизнеса – это около 17 месяцев ежедневных продаж или десять лет еженедельных. Но даже при 500 числах гистограмма получается неравномерной, с довольно большими вариациями. В данном случае одна пара цифр (68) не появляется совсем, а три пары (10, 53 и 74) встречаются в два раза чаще, чем ожидаемый 1 процент. Это нормальные отклонения, характерные для случайных данных.




