Теперь посмотрим на сфабрикованные данные.
Следующая гистограмма отображает распределение двух последних цифр в 500 числах, придуманных человеком. Более сильные вариации видны даже с первого взгляда. Две пары (93 и 94) встречаются более чем в 4 процентах чисел, что маловероятно для реальных данных. Двенадцать пар не встречаются вообще, и это тоже крайне маловероятно.
Задайте себе следующие три вопроса. Утвердительный ответ на любой из них должен усилить ваши подозрения.
a) По непонятной причине есть пара (или пары) цифр, встречающиеся чаще остальных?
б) Частота повторения сдвоенных цифр (особенно 00 и 55) меньше средней?
в) Убывающие пары (10, 21, 32, 43, 54, 65, 76, 87, 98) явно встречаются чаще других?
В приведенном примере ответ на вопрос (a) утвердителен. Кроме того, в массиве данных нет сдвоенных цифр (б). Приблизительно 10 процентов всех чисел должны оканчиваться на сдвоенные цифры. У нас таких 20 из 500, всего 4 процента. Пары 00, 55 и 77 вообще не встречаются.
Из 500 пар последних цифр 44 – убывающие. Это почти точно ожидаемые 9 процентов (из 100 возможных пар девять убывающие). Так, по критерию (в) данные не вызывают подозрений.
Наш набор данных не прошел два из трех тестов. Будь это суммы продаж мелкого бизнеса, стоило бы запросить дополнительную или более подробную информацию – и посмотреть, как отреагирует продавец.
Нет нужды беспокоиться, что вам придется считать вручную. На практике все это делается с помощью функций «копировать» и «вставить». Попросите данные в виде таблицы Excel или в совместимом с ней формате, чтобы без труда перенести их в шаблон теста, использующего закон Бенфорда. Примеры таких тестов можно бесплатно найти в интернете, в том числе один тест Нигрини (NigriniCycle.xlsx). Перенеся данные, выполните инструкции и заполните определенные столбцы заранее известными формулами. Результатом будут отформатированные гистограммы для двух последних цифр и итоги других распространенных тестов. Кроме того, программа вычисляет математическую оценку статистической значимости, что, конечно, гораздо надежнее простого просмотра полученных данных.
Резюме: Как распознать фальшивые числа
• Когда распределение цифр в последней группе данных отличается от обычного распределения, характерного для данной компании, это может быть признаком подлога.
• Растратчики и мошенники, придумывающие числа, неосознанно отдают предпочтение убывающим парам цифр (таким как 10, 21, 32 и так далее).
• Мошенники реже пользуются сдвоенными цифрами (например, 00 или 55), полагая, что они выглядят недостаточно «случайными».
12
Как распознать числа, которыми манипулировали
Один нью-йоркский страховой агент (фирма щедро оплачивала ему представительские расходы) оказался талантливым мошенником. Желая перейти на безбумажную документацию, его компания требовала сканы выписанных квитанций, а не сами квитанции. Страховой агент обнаружил: можно черной ручкой переправить в документе 1 на 7 или на 9, и на сканере с низким разрешением такое изменение незаметно.
Затем он пошел еще дальше и стал следить за тем, чтобы суммы, указанные в квитанциях, начинались с 1. Страховой агент мог позавтракать за 18 долларов и останавливаться в гостинице, где номер стоил 178 долларов. После этого он подправлял суммы и получал возмещение в размере 98 долларов за завтрак или 778 за гостиницу.
Одним росчерком пера он увеличил суточные расходы с 70 до 800. Но ему не повезло – аудиторский отдел страховой компании был одним из первых, применявших для анализа закон Бенфорда. В данном случае оказалось достаточно первых цифр, чтобы вызвать подозрения. Обнаружилось преобладание семерок и девяток и недостаток единиц. Расследование подтвердило факт обмана, и компания подала на страхового агента в суд, потребовав возмещения ущерба.
Подвергшиеся манипуляции числа могут представлять бо́льшую проблему, чем полностью выдуманные. В данном случае манипуляция означает, что кто-то ради личной выгоды уменьшил или увеличил реальную цифру. Изменение не обязательно должно быть таким грубым, как переправка 1 на 7. Зачастую достаточно достичь какого-то предела, цели или порога. Средства на представительские расходы обычно ограничены, при превышении либо не возмещаются суммы, либо требуются дополнительное подтверждение или документы. Можно ожидать, что предъявленные к возмещению цифры сосредоточатся чуть ниже границы.
«Это обычная практика для государственных чиновников», – заметил Марк Нигрини. Он изучил одно правительственное агентство. В нем сотрудникам выдавались закупочные карточки на сумму до 2500 долларов. Результат: «масса закупок на сумму 2500, 2499, 2496 долларов… Очевидно, это гениальные люди, которые говорили: “Не пишите 2501, пишите 2496 долларов. Я единственный из 35 000 правительственных чиновников знаю арифметику!” Однако все мы склонны думать как все, и поэтому каждый считает себя единственным».
Один из способов выявить исправления – проверка второй цифры. Сосчитайте, сколько раз каждая из десяти цифр встречается во втором знаке числа, справа от первой цифры. Для 74991 доллара вторая цифра – 4, и именно ее нужно учитывать при подсчете. Изобразите результаты в виде гистограммы.
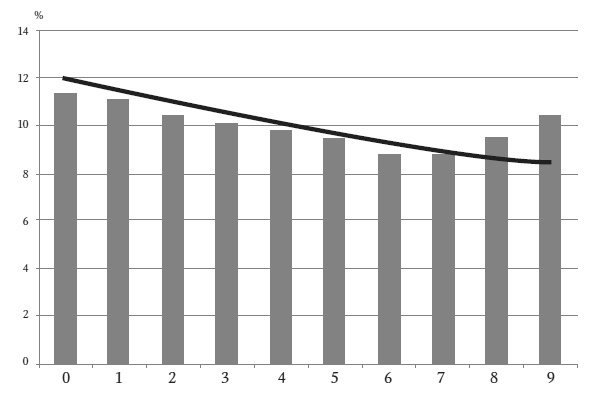
Вторые цифры: числа, подвергшиеся манипуляции
С реальными числами не следует ожидать слишком большой вариации в частоте вторых цифр. Закон Бенфорда предсказывает, что самой распространенной второй цифрой будет 0, с частотой появления 12 процентов, а реже всего должна встречаться 9 – в 8,5 процента случаев. Однако зачастую вы видите такую диаграмму, как представлена на рисунке на следующей странице. Сплошная линия – это идеальная кривая Бенфорда для вторых цифр, а столбики – реальные результаты подсчета. На первый взгляд разница не очень велика, однако она существенна. В столбиках показан избыток цифр 8 и 9, а также нехватка всех остальных. Это может произойти при «круглом» лимите, например, 1000 долларов. Обычно люди указывают расходы, немного не дотягивающие до порога.
Эффект порога – довольно распространенное явление, но не стоит делать поспешных выводов, когда вы сталкиваетесь с чем-то подобным. Наемный работник, знающий, что компания оплачивает расходы на еду до 50 долларов, может попробовать питаться на 49 с мелочью. Он не делает компании одолжение, а просто играет по установленным правилам.
С другой стороны, работник, преувеличивший расходы на еду – или фальсифицирущий их, – тоже имеет все основания не превышать установленного порога. Получив такие результаты, вы, возможно, захотите проверить поведение сотрудника – либо он представляет к оплате чеки, не превышающие порога, либо не переходит установленные границы, либо тут есть признаки подделки.

