И только когда вероятность чередования увеличивается до 90 процентов, большинство людей считают, что чередование слишком ритмично, чтобы быть случайным. Вот пример последовательности с уровнем чередования 90 процентов:

Это почти идеальная последовательность черного и белого. Встречается только два повторения одного и того же цвета подряд, причем длина – всего два квадрата.
Как и во всех других случаях, фокусники использовали эти идеи задолго до того, как о них написали психологи. Иллюзионисты давно знали, что честно перетасованная колода карт рискует показаться зрителям не случайной. В ней обязательно попадутся «подозрительные» группы похожих карт, например, четыре картинки подряд. Статистику это не покажется странным – в отличие от обычного человека.
В некоторых фокусах используется колода, выглядящая лучше, чем действительно перетасованная. Карточный аналог последовательностей с избытком чередования, нами они воспринимаются как случайные. В так называемой раскладке Си Стеббинса карты чередуются в строгом порядке: черная-красная-черная-красная-черная-красная. Масти во всей колоде тоже разложены не случайно: трефы-червы-пики-бубны. Значения следуют в таком порядке: Т–4–7–10–K–3–6–9–Д–2–5–8–В. Может сложиться впечатление, что эти закономерности взяты с потолка. Ничего подобного. Колода только выглядит случайной.
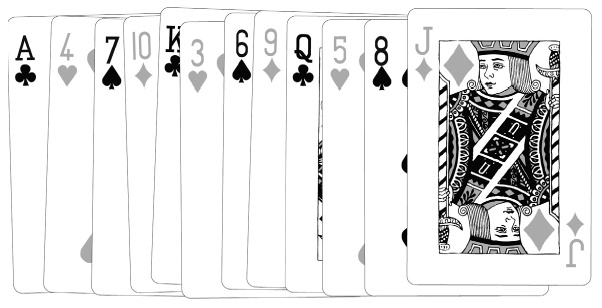
Раскладку Стеббинса запомнить просто, и в этом суть. Фокусник, видящий нижнюю карту снятой колоды, мгновенно вычисляет следующую… а она становится верхней картой вновь сложенной и выровненной колоды. При желании он может назвать эту карту, а также любую другую карту в колоде.
В большинстве случаев мы очень хорошо умеем обманывать сами себя. Поняв, что «легкая рука» – иллюзия, мы начинаем видеть ее примеры повсюду. Многие пользователи iPod жалуются, что функция воспроизведения в случайном порядке работает не так, как должна. Это не может быть случайным – только что плеер проиграл четыре песни Лил Уэйн подряд! Но такие серии должны встречаться. Дефект не в программе, а у нас в голове.
Расписание автобусов на оживленных улицах Манхэттена почти ничего не означает, потому что из-за плотного потока транспорта и многочисленных светофоров автобусы приходят практически в случайном порядке. Однако график движения совсем не выглядит случайным. Создается впечатление, что ты ждешь автобуса 20 минут, а затем сразу приходят два или три подряд.
Специалист по когнитивной психологии Стивен Пинкер сообщает об эксперименте. Добровольцы должны нажимать кнопку, услышав звуковой сигнал. Участники эксперимента знали, что сигналы будут поступать в случайном порядке. Они жаловались, что машина неисправна: «Сигналы приходят пачками. Вот так: бип-бип-бип-бип-бип… бип… бип-бип… бип-бип-бип-бип-бип». Они не понимали, как выглядит случайность, объясняет Пинкер.
Когда легкая рука проявляется в двух или трех пространственных измерениях, а не только в одном, временном, это называется иллюзией кластеризации. Во время воздушных налетов на Лондон ходили слухи, что немецкие бомбы не попадают в кварталы, где живут нацистские шпионы. Карты показывали группы попаданий в одни районы и ни одного попадания в другие. Британская разведка восприняла эти слухи достаточно серьезно, разделила карту Лондона на квадраты и тщательно следила, куда падают бомбы. В результате они пришли к выводу, что бомбы действительно падают случайно. Статистик Уильям Феллер заметил: «Нетренированному глазу случайность видится как регулярность или тенденция к образованию групп». Многие отказывались верить. Как спрашивал Чико Маркс
[17]
: «Ты веришь мне или своим глазам?»
На первый взгляд вера в легкую руку противоречит более известному «заблуждению игрока». 18 августа 1913 г. в казино Монте-Карло «черное» выпало 26 раз подряд. Примерно после 15-го раза об этом стало известно всем посетителям. Игроки побросали карты и игральные кости, и у стола с рулеткой собралась целая толпа. Большинство желали поставить на «красное». Они верили, что после стольких «черных» подряд вероятность того, что в следующий раз выпадет «красное», выше обычной. Когда это убеждение опровергалось – после того, как вслед за остановкой колеса в очередной раз выпадало «черное» – многие удваивали ставку, убежденные, что в следующий раз вероятность «красного» еще выше.
Заблуждение игрока – это вера, что случайный результат, не выпавший в прошлом, с большей вероятностью случится в ближайшем будущем. Это обоснованное заблуждение («я давно уже должен выиграть!» – думает каждый неудачник), но все-таки заблуждение, побуждающее неудачников продолжать игру, не учась на ошибках. Будь у любителей азартных игр хотя бы инстинкт самосохранения, как у крыс, преодолевающих лабиринт, они бы поняли: когда я играю, ничего хорошего не происходит. Вместо этого они продолжают делать ставки и в ответ на проигрыш могут даже поднимать их. К сожалению, колесо рулетки не может знать, что именно эти люди должны выиграть. Шансы остаются прежними.
Вполне возможно, что вы уже запутались. Создается впечатление, что я утверждаю: люди верят в продолжение победных серий… за исключением случаев, когда они верят в прямо противоположное. Ничего подобного. Заблуждение игрока и теория легкой руки – две стороны одной медали. И то, и другое – следствие «закона малых чисел».
Это полушутливое правило сформулировали в 1971 г. Амос Тверски и Дэниел Канеман. Оно гласит:
«Интуиция людей относительно случайной выборки, похоже, подчиняется закону малых чисел, гласящему, что закон больших чисел также применим и к малым».
Чтобы понять его смысл и оценить шутку, нужно знать, что такое «закон больших чисел». Это одна из главных формул вероятности. Когда я подбрасываю монету, то орел и решка не обязательно выпадут одинаковое число раз. Для этого потребуется очень длинный случайный процесс. Но если я бросаю монету большое количество раз, то пропорция орлов приближается к ожидаемой величине (50 процентов).
Закон больших чисел утверждает, что от очень маленькой выборки нельзя ожидать, что она будет отражать процесс в целом. Мы все об этом знаем и иногда шутим на эту тему (даже неспециалисты). Средняя американская семья состоит из 2,6 человека. Но кто мог бы себе представить такое в реальности?
Закон малых чисел Тверски и Канемана применим в области психологии. Он гласит, что мы безосновательно ждем от маленькой выборки отражения реальной ситуации. Если подбросить монету десять раз, то закон больших чисел свидетельствует о возможности получить смещенный результат, например, семь решек и три орла. Но люди думают иначе. Покажите им монетку, на их глазах семь раз из десяти упавшую решкой вверх, и большинство скажет, что с монетой что-то не так.




