Если вы хорошо поняли сказанное, то решите, нельзя или можно начертить одним росчерком те три фигуры, которые здесь показаны.
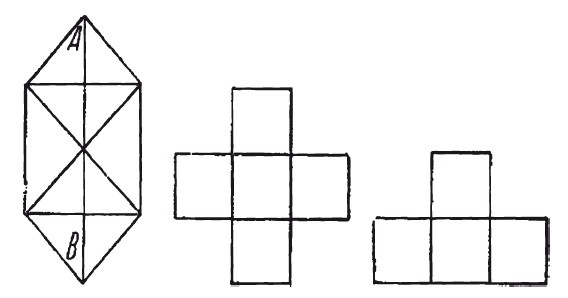
62. Может ли это быть?
Перед вами морской вид. Не правда ли, художник очень странно изобразил на нем лунный серп: вместо того чтобы висеть на небе, серп плавает на воде, как лодка. Может ли это быть? Не ошибся ли художник?

63. Путешествие по островам
Здесь вы видите карту морского залива. Четыре островка соединены между собою и с берегами мостами. Вам дается задание: побывать на берегу и на всех островах, пройдя непременно через все мосты и притом только по одному разу.

Кто сообразит, какая связь между этой задачей и предыдущей, тот легко догадается, разрешима ли она.
Итак, укажите правильный маршрут, если вы думаете, что он существует. Откуда вы советуете начать путешествие?
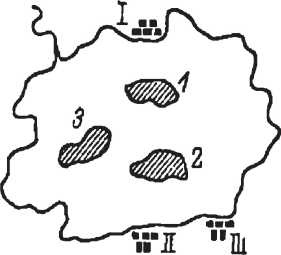
64. Три острова
На озере три острова, которые отмечены на чертеже цифрами 1, 2 и 3. А на берегу расположено три рыбачьих поселка: I, II и III. Лодка отплывает из поселка I, посещает острова 1 и 2 и пристает к поселку II. Одновременно из поселка III отплывает другая лодка, пристающая к острову 3. Пути обеих лодок не пересекаются.
Можете ли вы начертить эти пути?
65. Что шире и что выше?
Какая из этих двух фигур шире и какая выше? Дайте ответ, не измеряя фигуру бумажкой, а прямо на глаз (как говорится, «по глазомеру»).

66. Три толстяка
Рассмотрите рисунок и сравните на глаз длину трех человеческих фигур.

Попробуйте сказать, насколько фигура человека, идущего впереди всех, разнится от фигуры идущего сзади.
Когда вы это сделаете, возьмите полоску бумаги и смерьте толстяков. Вы будете поражены: вы ожидали, что длиннее всех задняя фигура, между тем она-то и оказывается самой короткой. Перед вами один из обманов зрения.
67. На какой ноге?
На какой ноге стоит футболист – на правой или на левой?
По-видимому, он стоит на правой ноге; но с такой же уверенностью можно утверждать, что он стоит на левой ноге.

Сколько ни всматривайтесь в рисунок, вы этого вопроса не решите. Художник так искусно замел следы, что вам ни за что не установить, какую ногу поднял футболист и на какую он опирается – на правую или на левую.
Вы спросите: «На какую же, в конце концов?» Я и сам не знаю. Да и художник не знает – забыл. Так это и останется навеки неразрешимой тайной.
68. Одним росчерком
Вы, наверное, не подозреваете, что одним росчерком, не отрывая пера от бумаги, можно рисовать довольно сложные картинки. Взгляните, какие замысловатые рисунки изобразил этим манером иллюстратор книги на с. 93: тут и большой океанский пароход, и флаг, и парусник, и красноармеец на коне, и голубь, на крыле которого изобретательный художник ухитрился запечатлеть мою фамилию.
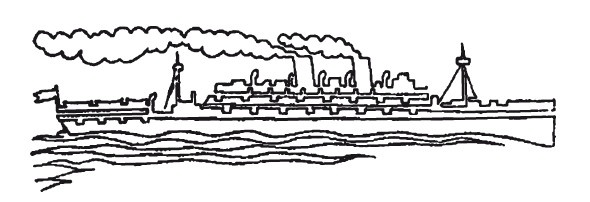


69. Много ли рыбы?
Здесь вы видите загадочный рисунок. Рыболов как будто еще ничего не выудил. Но, вглядевшись хорошенько в очертания рисунка, вы убедитесь, что улов довольно обилен: три большие рыбины уже пойманы. Где же они?

70. Фигурки-головоломки
Игра, о которой пойдет речь, имеет очень древнее происхождение. Она древнее, чем шахматы, хотя и не так хорошо известна. Ее родина – Китай; здесь она зародилась четыре тысячелетия назад. Впрочем, первоначально это была не игра, а способ обучения начаткам геометрии.
Сущность этой игры в том, что из семи определенных геометрических фигур складывают различные силуэты. Те семь кусочков, которые служат для складывания, вырезаются из плотного картона или выпиливаются из дерева. Все они составляют части квадрата; разрезают квадрат так, как показано белыми линиями (см. верхний рисунок на с. 96).
Получают:
2 больших треугольника,
1 треугольник средней величины,
2 малых треугольника,
1 квадратик,
1 параллелограмм (косой четырехугольник).
Первая задача состоит в том, чтобы из разрозненных кусочков вновь составить первоначальный квадрат. Это не так легко, как кажется, и удается далеко не сразу (если складывать, не глядя на чертеж).
Выполнив это, можно приступить к складыванию силуэтов. Как они составляются, показано на примере петушка и гуся (с. 96). Кусочки надо прикладывать один к другому вплотную, без промежутков; на рисунках промежутки оставлены лишь для наглядности.
Правила складывания таковы:
1) кусочки не должны хотя бы частью прикрывать друг друга;

