Четырьмя двойками (79)
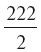 = 111
= 111
Четырьмя тройками (80)

Мы привели здесь решения только до 6. Остальные придумайте сами. Да и указанные решения можно составить и другими комбинациями троек.
Четырьмя четверками (81)
Который год? (82)
Будет только один такой год в XX веке: 1961-й.
В зеркале (83)
Единственные цифры, которые не искажаются в зеркале, – это 1, 0 и 8. Значит, искомый год может содержать в себе только такие цифры. Кроме того, мы знаем, что это один из годов XIX века, т. е. что первые его две цифры 18.
Легко сообразить теперь, какой это год: 1818-й. В зеркале 1818 год превратится в 8181-й: это ровно в 4½ раза больше, чем 1818:
1818 × 4½ = 8181.
Других решений задача не имеет.
Какие числа? (84)
Ответ прост: 1 и 7. Других таких чисел нет.
Сложить и перемножить (85)
Таких чисел сколько угодно:
3 × 1 = 3; 3 + 1 = 4;
10 × 1 = 10; 10 + 1=11
и вообще всякая пара целых чисел, из которых одно – единица.
Это потому, что от прибавления единицы число увеличивается, а от умножения на единицу остается без перемены.
Столько же (86)
Числа эти 2 и 2. Других целых чисел с такими свойствами нет.
Три числа (87)
1, 2 и 3 дают при перемножении и при сложении одно и то же:
1 + 2 + 3 = 6; 1 × 2 × 3 = 6.
Умножение и деление (88)
Таких чисел очень много. Например:
2: 1 = 2; 2 × 1 = 2;
7: 1 = 7; 7 × 1 = 7;
43: 1 = 43; 43 × 1 = 43.
Вдесятеро больше (89)
Вот еще четыре пары таких чисел:
11 и 110; 14 и 35; 15 и 30; 20 и 20.
В самом деле:
11 × 110 = 1210; 15 × 30 = 450;
11 + 110 = 121; 15 + 30 = 45;
14 × 35 = 490; 20 × 20 = 400;
14 + 35 = 49; 20 + 20 = 40.
Других решений задача не имеет. Довольно хлопотливо разыскивать решения вслепую. Знание начатков алгебры значительно облегчает дело и дает возможность не только отыскать все решения, но и удостовериться, что больше пяти решений задача не имеет.
На что он множил? (90)
Рассуждаем так. Цифра 6 получилась от сложения колонки из двух цифр, из которых нижняя может быть либо 0, либо 5. Но если нижняя 0, то верхняя 6. А может ли верхняя цифра быть 6? Пробуем: оказывается, чему бы ни равнялась вторая цифра множителя, никак не получается 6 на предпоследнем месте первого частного произведения. Значит, нижняя цифра предпоследней колонки должна быть 5; тогда над ней стоит 1.
Теперь легко восстановить часть стертых цифр:
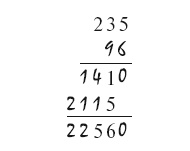
Последняя цифра множителя должна быть больше 4, иначе первое частное произведение не будет состоять из четырех цифр. Это не может быть цифра 5 (не получается 1 на предпоследнем месте). Пробуем 6 – годится. Имеем:
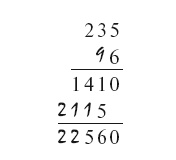
Рассуждая далее подобным же образом, находим, что множитель – 96.
Пять пятниц (91)
Пять пятниц может быть в феврале високосного года (т. е. когда февраль имеет 29 дней). А именно если первая пятница будет 1 февраля, то
8 февраля………………… вторая пятница,
15 февраля………………. третья пятница,
22 февраля………………. четвертая пятница,
29 февраля………………. пятая пятница.
Итого в течение этого короткого месяца будет пять пятниц.
Сестры и братья (92)
Всех семеро: четыре брата и три сестры. У каждого брата три брата и три сестры; у каждой сестры четыре брата и две сестры.
Сколько детей? (93)
Всех детей семь: шесть сыновей и одна дочь. (Обычно же отвечают, что детей двенадцать; но тогда у каждого сына было бы шесть сестер, а не одна.)
Завтрак (94)
Дело объясняется очень просто. Село за стол не четверо, а только трое: дед, его сын и внук. Дед и сын – отцы, а сын и внук – сыновья.
Сколько им лет? (95)
Рассчитать, сколько лет каждому, нетрудно. Ясно, что сын старше внука в 7 раз, а дед – в 12 раз. Если бы внуку был 1 год, сыну было бы 7 лет, деду – 12 лет, а всем троим вместе 20 лет. Это ровно в 5 раз меньше, чем на самом деле. Значит, в действительности внуку 5 лет, сыну 35 и деду 60.
Проверим: 5 + 35 + 60 = 100.
Землекопы (96)
На удочку этой задачи легко попасться: можно думать, что если 5 землекопов в 5 часов вырыли 5 метров канавы, то для выкопки в 100 часов 100 метров понадобится 100 человек. Однако это совершенно неправильное рассуждение: понадобятся те же 5 землекопов, не больше.
В самом деле: 5 землекопов в 5 часов выкапывают 5 метров; значит, 5 землекопов в 1 час вырыли бы 1 метр, а в 100 часов – 100 метров.
Сколько партий? (97)
Обычно отвечают, что каждый играл по одному разу, не соображая, что трое (и вообще нечетное число) игроков никак не могут играть каждый только по одному разу. С кем же тогда играл третий игрок? В каждой партии должны ведь участвовать два партнера. Если играли А, В и С и сыграно было три партии, то это значит, что играли

