В чем обман (110)
Прохожий подсчитал выручку неверно. Он принимал, что первая крестьянка продала столько же пар яиц, сколько вторая – троек: тогда средняя цена действительно была бы 10 коп. за 5 штук, или 2 коп. штука. На самом деле, однако, первая продала 15 пар, вторая же – всего 10 троек. Дорогих яиц продано было больше, чем дешевых, и средняя цена была выше 2 коп. за штуку. Истинная выручка равна:
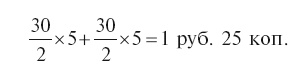
Бой часов (111)
Если часы делают в 3 секунды 3 удара, т. е. если 2 промежутка между ударами длятся 3 секунды, то продолжительность одного промежутка – 1½ секунды. При 7 ударах имеется 6 промежутков. Считая по 1½ секунды на каждый промежуток, имеем, что 7 ударов часы должны делать в 6 × 1½ = 9 секунд.
Мишины котята (112)
Нетрудно понять, что ¾ котенка есть четвертая доля всех котят.
Значит, всех котят было вчетверо больше, чем ¾, т. е. три. Действительно, ¾ от трех составляет 2¼, и остается ¾ котенка.
Кошки (113)
Соображаем:
4 кошки и 3 котенка весят 15 килограммов.
3 кошки и 4 котенка весят 13 килограммов.
Значит, 7 кошек и 7 котят весят 28 килограммов. Отсюда узнаем вес одной взрослой кошки вместе с одним котенком – 4 килограмма. Теперь узнаем, сколько весят 4 кошки и 4 котенка: умножив 4 килограмма на 4, получаем 16 килограммов.
Сопоставляем:
4 кошки и 3 котенка весят 15 килограммов.
4 кошки и 4 котенка весят 16 килограммов.
Ясно, что котенок весит 1 килограмм, и, следовательно, вес взрослой кошки – 3 кило.
Сколько квадратов? (114)
Значит, фигура заключает 55 различно расположенных квадратов 5 различных размеров.
Квадратный метр (115)
В тот же день Алеша убедиться в этом никак не мог. Даже если бы он считал круглые сутки непрерывно, то и тогда насчитал бы в сутки только 86 400 клеточек.
Ведь в 24 часах всего 86 400 секунд. Ему надо было бы считать без перерывов почти 12 дней, а по 8 часов в сутки – целый месяц, чтобы досчитать до миллиона.
Задача о волосах (116)
Среди школьников наверняка имеются даже не двое, а целые десятки ребят с одинаковым числом волос. Это следует из того, что число всех школьников больше, чем число волос на голове каждого на них. Школьников с различным числом волос может быть не более 200 000.
Как поделить яблоки? (117)
Яблоки были разделены таким образом. 3 яблока разрезаны были каждое пополам; получилось 6 половинок, которые и роздали ребятам. Остальные 2 яблока разрезали каждое на 3 равные доли; получилось 6 третьих долей, которые тоже роздали ребятам. Каждому мальчику было дано, значит, по одной половине и по ⅓ доле яблока, т. е. все ребята получили поровну.
Как видите, ни одно яблоко не было разрезано больше чем на три равные части.
Почтовые марки (118)
Эта задача имеет только одно решение. Гражданин купил:
50-копеечных марок………………..1 штуку
10-копеечных марок………………..39 штук
1-копеечных марок…………………60 штук
Действительно:
всех марок 1 + 39 + 60 = 100 штук.
А стоят они:
50 + 390 + 60 = 500 копеек.
Сколько монет? (119)
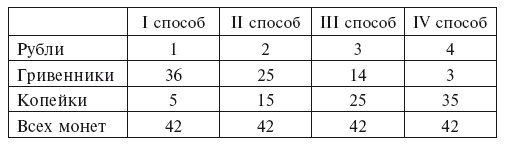
Задача имеет четыре решения. Вот они:
Почем лимоны? (120)
Мы знаем, что 36 штук лимонов стоят столько рублей, сколько на 16 рублей дают лимонов. Но 36 штук стоят:
36 × (цену штуки).
А на 16 рублей дают штук:
Значит:
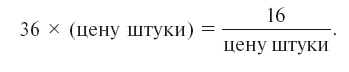
Если бы правую часть не делили на цену штуки, то в левой части получили бы больше в (цену штуки) раз, т. е. 16:
36 × (цену штуки) × (цену штуки) = 16.
Если бы левую часть не множили на 36, то в правой части получили бы меньше в 36 раз:
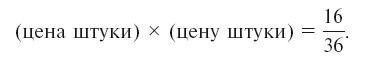
Ясно, что цена штуки =
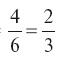руб., а стоимость дюжины лимонов = ⅔ × 12 = 8 руб.
Книжный червь (121)
Обычно отвечают, что червь прогрыз 900 + 800 страниц да еще две крышки переплета. Но это не так. Поставьте рядом две книги: первую налево, вторую направо, как показано на рисунке на с. 119. И тогда посмотрите, сколько страниц между первой страницей первой книги и последней страницей второй книги. Вы убедитесь, что между ними нет ничего, кроме двух крышек переплета.
Книжный червь испортил, значит, только переплеты книг, не тронув их листов.
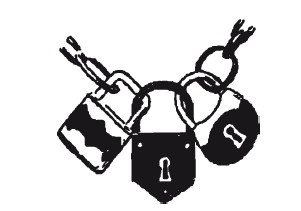
Одна лодка на троих (122)
Замки должны быть продеты один сквозь другой, как показано на рисунке. Легко видеть, что эту цепь из трех замков каждый владелец может разнять и вновь замкнуть своим ключом.
Из шести спичек (123)
Вы, вероятно, пытались составить плоскую фигуру из шести спичек, и, конечно, безуспешно, потому что так задача неразрешима. Но ведь никто не мешает вам располагать треугольники в пространстве. И тогда она решается очень просто: стоит лишь построить из шести спичек пирамидку. У вас получается тогда четыре равносторонних треугольника из шести спичек.
