Графики других типов событий выглядят иначе. Возьмем продолжительность жизни. Шансы умереть достаточно высоки в момент рождения – некоторые младенцы погибают, едва появившись на свет, – но если ребенок благополучно прожил первый год, то, скорее всего, он проживет еще несколько десятков лет. После 40 лет шансы умереть начинают повышаться. После 50 лет вероятность смерти резко возрастает с каждым годом, достигая максимума примерно в 82 года. Это и есть средний возраст смерти.
Продолжительность жизни придерживается нормальной, или гауссовой, кривой распределения. График выглядит так:
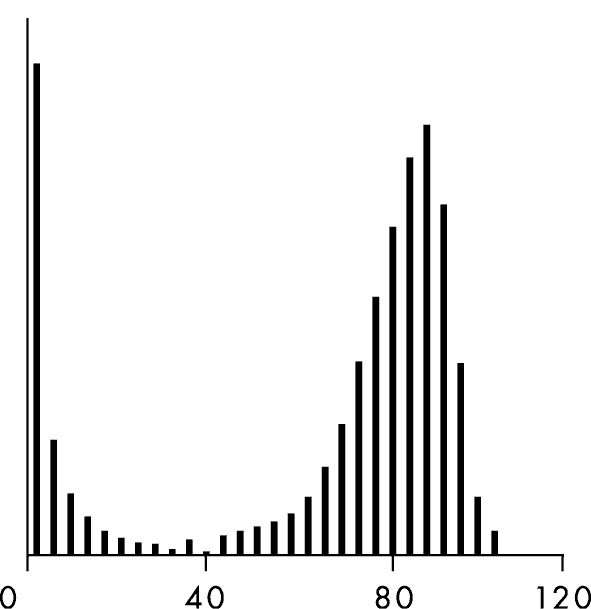
Продолжительность жизни
Большинство людей интуитивно понимают: для прогнозирования различных видов событий нужны разные виды рассуждений. Мы знаем, что кассовые сборы и продолжительность жизни требуют разных типов оценок, даже если нам ничего не известно о медицинской статистике или тенденциях в индустрии развлечений. Тененбаум и Гриффитс хотели выяснить, откуда берутся эти интуитивные знания. Поэтому они выбрали события с четкими закономерностями: от кассовых сборов и продолжительности жизни до средней длины стихотворений, продолжительности карьеры конгрессмена (которая придерживается распределения Эрланга) и времени пребывания пирога в духовке (которое лишено четко выраженных закономерностей)
[232].
Затем они попросили сотни студентов предсказать будущее на основании одного фрагмента данных:
Вы читаете о фильме, который собрал на сегодняшний день 60 миллионов долларов. Сколько он соберет в итоге?
Вы встречаете человека, которому 39 лет. Как долго он или она будет жить?
Пирог печется уже 14 минут. Сколько времени он должен оставаться в духовке?
Вы встречаете американца, который является членом конгресса уже 11 лет. Сколько лет он прослужит в конгрессе в общей сложности?
[233]
Никакой дополнительной информацией студенты не располагали. Им ничего не рассказали ни о степенном распределении, ни о кривых Эрланга. Их просто попросили сделать прогноз, основанный на одном фрагменте данных без каких-либо подсказок касательно типов вероятностей.
И все же прогнозы участников оказались поразительно точны. Они знали, что фильм, который собрал 60 миллионов, – это блокбастер, который, скорее всего, соберет еще 30 миллионов. Интуиция подсказывала им, что человек, которому стукнул четвертый десяток, вероятно, проживет еще лет 50. Они догадывались, что конгрессмен, который находился у власти в течение 11 лет, наверняка прослужит еще лет шесть или около того: несмотря на то, что длительный срок пребывания в должности дает свои преимущества, даже видные законодатели могут пострадать от новых политических веяний.
В ответ на заданные вопросы лишь немногие из участников сумели описать логику, которой они пользовались при прогнозировании. Они просто давали те ответы, которые казались правильными. В среднем их прогнозы зачастую отличались от правильного ответа менее чем на 10 %. На самом деле, когда Тененбаум и Гриффитс графически представили все предсказания студентов по каждому вопросу, полученные кривые распределения почти идеально соответствовали реальным закономерностям, которые обнаружили профессоры в данных из интернета.
Кроме того, каждый студент интуитивно понимал, что различные виды предсказаний требовали различных видов рассуждений. Это было очень важно. Они понимали – хотя и не обязательно осознавали почему, – что продолжительность жизни имеет форму нормальной кривой, тогда как кассовые сборы, как правило, подчиняются степенному закону.
Некоторые исследователи называют эту способность интуитивно улавливать закономерности «байесовским мышлением» или «байесовской психологией». Дело в том, что для подобных прогнозов компьютер использует ту или иную разновидность правила Байеса
[234] – математическую формулу, которая обычно требует анализа тысяч моделей одновременно и сравнения миллионов результатов
[235]. В основе правила Байеса лежит следующий принцип: даже при наличии очень малого количества данных прогнозирование будущего возможно. В этом случае нам придется скорректировать наши предположения с учетом наблюдений за окружающим миром. Допустим, ваш брат говорит, что идет ужинать с другом. Поскольку большинство друзей вашего брата мужского пола, вы можете предположить, что он собирается встретиться с мужчиной с вероятностью 60 %. Теперь вообразим, что ваш брат говорит, что этот друг – коллега по работе. В этом случае вы, скорее всего, измените свой прогноз, ибо знаете, что большинство коллег вашего брата женского пола. Правило Байеса позволяет вычислить точную вероятность того, что ваш брат будет ужинать с женщиной или мужчиной, на основании всего одного или двух фрагментов данных и ваших предположений
[236]. Чем большим количеством информации вы располагаете – его друга зовут Пэт, он или она любит приключенческие фильмы и модные журналы, – тем точнее вы сможете вычислить вероятности.



