Ответ прост: качество управления улучшилось, если улучшились параметры более приоритетных (информационных) элементов векторов и качество управления ухудшилось, если значения этих параметров ухудшилось. Ещё раз отметим: улучшение/ухудшение параметров векторов, имеющих более высокий приоритет рано или поздно, но неизбежно приводит к соответствующему изменению значений в менее приоритетных элементах векторов.
Следует подчеркнуть, что в соответствии с U-законом неразрывности переход системы с одного в другой режим может осуществляться только последовательно, страта за стратой, поэтому при переводе системы из адаптационного режима в точке С в режим сильного манёвра по умолчанию подразумевается вначале перевод системы в режим слабого манёвра, и только затем в область сильного манёвра. Аналогично и в точке D после осуществления сильного манёвра система по умолчанию должна перейти в режим слабого маневра, затем в адаптационный режим, и лишь после этого она может работать в программном режиме.
Диапазон колебаний траектории программного режима работы определяется главным образом «материальными» ограничениями конструкции системы. Диапазон колебаний траектории адаптивного режима работы определяется главным образом «материальными» ограничениями настраиваемых элементов системы. Диапазон колебаний траектории «слабого манёвра» определяется глубиной и сложностью предикционного расчёта. Диапазон колебаний траектории «сильного манёвра» определяется интеллектуальным уровнем, определяющим возможности суперсистемы к прогностике.
Привязка режимов управления к типологизации систем управления показывает их однозначное соответствие (рис. 6.8). Программный и адаптивный тип СУ – это балансировочные режимы работы, прогностический (предикционный) и интеллектуальный – это манёвры супер/систем.

Рис. 6.8. Соответствие типа СУ режимам управления классов 4U и 2U
Конечно же, данная стратификация не является догмой: универсумный подход позволяет детализировать это описание, разбив его на пять, шесть, восемь, сто двадцать восемь и любое другое количество уровней в зависимости от требований к точности описания систем различной сложности. Универсумный подход позволяет более точно представить и однозначно связать между собой описание различных схем, режимов, систем, областей состояний и критериев качества процесса управления.
6.3. Гибкость и устойчивость и управления
Скорость перехода системы с одного режима работы на другой определяет гибкость рассматриваемой системы управления.
Одно из наиболее распространённых и традиционных определений понятия «гибкость» подразумевает «свойство алгоритма, определяемое возможностью его адаптации к изменениям входной информации без изменения решаемой задачи» [53, 69]. С универсумной точки зрения понятие «гибкость» определяется способностью системы в зависимости от конкретного набора входных воздействий S обеспечивать своевременное переключение между различными режимами (схемами) управления для получения необходимой реакции R. Это переключение организует высшая освоенная данным универсумом страта управления. В практическом аспекте гибкость – это набор параметров (скорость, энергопотребление, импульсная мощность и др.), определяющих способность системы к переключению между режимами управления с целью сохранения устойчивости функционирования во внешней среде.
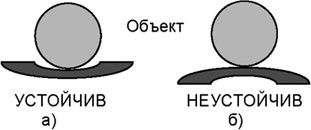
Рис. 6.9. Устойчивость объекта на поверхности различного типа
Что касается понятия «устойчивости», то, как известно, в большинстве отраслей науки и в технике понятие «устойчивость» построено на основе присущей объекту тенденции возвращаться к исходному режиму существования по всем (или по части)
параметрам, характеризующим его поведение, после того, как возмущающее воздействие, вызвавшее первоначальное отклонение параметров, будет снято. Периодические колебания приведут систему «шар-тарелка» в точку равновесия – устойчивости (рис. 6.9а). Отсутствие такой тенденции или наличие противоположной тенденции определяется как «неустойчивость». В этом случае отклонение шара от точки равновесия лишит систему «шар-тарелка» устойчивости (рис. 6.9б). то есть, в классической точке зрения устойчивая система просто должна «отработать» влияние внешнего фактора и вернуться на расчётную траекторию. Неустойчивая система самостоятельно возвратиться на заданную траекторию после снятия внешнего воздействия не может.
Следует также отметить, что традиционный подход обходит молчанием вопрос возможных отклонений траектории движения системы в случае отсутствия внешнего воздействия (наличия предельно ровной поверхности «тарелки»), ограничивая ответ некоторыми случайным и несущественными «девиациями».
Очевидно, что различные схемы управления для одних и тех же объектов в одних и тех же условиях обеспечивают как различную гибкость реагирования на возмущающие воздействия, так и различный максимально достижимый уровень устойчивости и качества управления.
Более полное раскрытие термина «устойчивость управления» требует рассмотрения различных траекторий достижения системами целевой функции в связи с их фазовыми характеристиками. Вопрос устойчивости процесса управления тесно связан с алгоритмикой работы схем, по которым оно осуществляется, с соотношением фазовых величин ОС восходящего и ПС нисходящего U-потока, образующих внутренние интегративные U-потоки положительной обратной связи (ПОС) и отрицательной обратной связи (ООС). В модели и терминологии импульсных и колебательных процессов этим связям будут соответствовать определённые траектории поведения системы.
Работа программной схемы (рис. 6.10а), реагируя на строго определённые входные состояния системы S, «вмешивается» в процесс управления преимущественно однозначным, дискретным способом. На траектории поведения системы чаще всего это может отражаться как «точка перелома». После осуществления программной реакции R система переходит в режим ожидания очередного однозначно определённого состояния S для выдачи соответствующей ему реакции R. Реакция на состояния системы, не предусмотренные программой, не осуществляется, балансный режим выполняется только в узких рамках набора запрограммированных SR-пар типа «Известный стимул – Соответствующая реакция» (УФУ-1).
Работа адаптивной схемы (рис. 6.10б) в классическом варианте описания поведения объекта при внешнем воздействии на него может быть представлена в виде некоторого отклонения от процесса идеального поведения с последующим возвращением на траекторию, близкую к идеальному режиму управления. Колебательный процесс траектории поведения объекта вокруг заданной траектории соответствует поведению шара в тарелке. Именно этот процесс классической теории управления признаётся критерием устойчивого поведения систем «по Ляпунову» (УФУ-3). Адаптивная схема реагирует на внешние воздействия с небольшим фазовым запаздыванием, она охвачена менее глубокой ООС.

