– Программную (конструктивно-механическую);
– Адаптивную (классическую, «ляпуновскую»);
– Предикционную (расчётно-предсказуемую);
– Прогностическую (вероятностно-интеллектуальную).
В классификации 2U можно говорить не только о балансировочном режиме для нижних страт и режиме манёвров для верхнмх, но и о пассивном поведении нижних универсумных страт и активном верхних; управляемости нижних страт и самоуправляемости верхних и так далее. В более широком смысле можно обратить также внимание на тот факт, что именно между адаптивной и предикционной системами проходит граница между растительным и живым (животным) миром: живое отличается от растительного именно способностью к предикционному расчёту и прогностике.
Универсумное описание максимально уточняет требования, предъявляемые к режимам и манёврам, осуществляемым различного типа системами управления и к траекториям, описывающим поведение этих систем в процессе управления. Так, сложные технические системы, например, автомобиль, самолёт, тот же российский Луноход или американский Марсоход могут работать в одной из трёх алгоритмик – программной, адаптивной (балансировочный режим удержания на курсе) и даже по схеме «предиктор-корректор» (слабый манёвр – уход от некоторой неожиданной помехи на курсе). Это, конечно же, не означает, что такие системы как автомобиль или самолёт наделены интеллектом. Они – воплощение Интеллекта, интегранты, управляемые суперсистемой, но не сам Интеллект. По схеме «предиктор-корректор» Марсоход может объехать скатившийся с откоса камень (совершить слабый манёвр), но если он неожиданно наткнётся на яму или другое препятствие, то он запрограммировано (что было сделано заранее Интеллектом) остановится, ожидая оперативного вмешательства Интеллекта (сильного манёвра) со стороны Центра управления.
Отдельного внимания заслуживает «межеумочная» граница перехода систем адаптивного управления в системы предикционного класса, в которых соблюдается мера примерного равенства фаз и амплитуд материальных и информационных составляющих U-потоков прямой и обратной связи. Такая «плавающая» случайным образом фаза может сделать систему предельно чувствительной к самым минимальным дифференциациям фазовых, амплитудных и частотных характеристик U-потока. В какой-то момент времени получить случайное преимущество может ОС. Тогда система будет работать по адаптивной схеме (или даже «застынет» в программном режиме работы). В другой момент времени преимущество может получить ПС и система может обнаружить свойства избирательности (и даже перейти в режим автоколебаний). Это эквивалентно нахождению системы в состоянии случайных перетоков U-потока по каналам отрицательной и положительной связи. Траектория поведения такой системы в обычном масштабе координат трудно предсказуема – «неравновесна», что дало некоторым философским школам повод для введения в понятийный оборот якобы нового природного явления – «порядка, возникающего из хаоса», чаще всего связываемого с понятием синергетики «точка бифуркации»[172].
Чаще всего примитивное понимание зависимости качества от сложности структурных отношений ОЯП проявляется в признании современными философами некоего «синергетического эффекта», под которым при выполнении людьми некоторых совместных работ подразумевается появление из неоткуда некой волшебной (а реально – не учитываемой ранее) энергии, разумно помогающей людям в осуществлении их желаний. Кроме того, понятие бифуркации используется в качестве веского аргумента подтверждения «тотально конструктивной роли случайности и хаоса», распространяемого на множество «труднообъяснимых», но вполне соответствующих описанию хаоса, турбулентности и прочих завихрений в смысловом наполнении гуманитарных дисциплин – философии, социологии, политологии и в других науках.
В синергетике убедительно показано, что современная наука имеет дело с очень сложноорганизованными системами разных уровней организации, связь между которыми осуществляется через взаимопереходы хаоса и гармонии. Отличие синергетического взгляда от традиционного диалектического, очевидно, состоит в переходе от исследования простых систем к сложным, от закрытых к открытым, от линейности к нелинейности (сложным траекториям развития), от равновесных форм к неравновесным, от господства стабильности к господству нестабильности [29, 24].
Популярен ещё один термин – «синергетический эффект», под которым чаще всего подразумевается волшебный результат взаимодействия двух и более факторов, при котором их суммарное действие превосходит эффект каждого отдельного компонента в виде их суммы. Это укоренившееся в научном сленге словосочетание является лишь бледной тенью более подробного и логичного описания эффекта, сделанного ещё в начале XX века А. А. Богдановым.
…загадка решается просто – надо только представить организуемые активности вместе с теми сопротивлениями, которые они преодолевают…
Итак, организованное целое оказалось на самом деле практически больше простой суммы своих частей, но не потому, что в нем создавались из ничего новые активности, а потому, что его наличные активности соединяются более успешно, чем противостоящие им сопротивления.
Наш мир есть вообще мир разностей; только разности напряжений энергии проявляются в действии, только эти разности имеют практическое значение. Там, где сталкиваются активности и сопротивления, практическая сумма, воплощенная в реальных результатах, зависит от способа сочетания тех и других; и для целого эта сумма увеличивается на той стороне, на которой соединение более стройно или «гармонично», заключает меньше «противоречий». Это и означает более высокую организованность [7].
Для установления более точного универсумного соответствия между схемами и системами управления, траекториями их поведения и устойчивостью следует рассмотреть границы областей устойчивого, неустойчивого, допустимого, недопустимого и других видов управления, рассматриваемых различными научными школами (рис. 6.14).
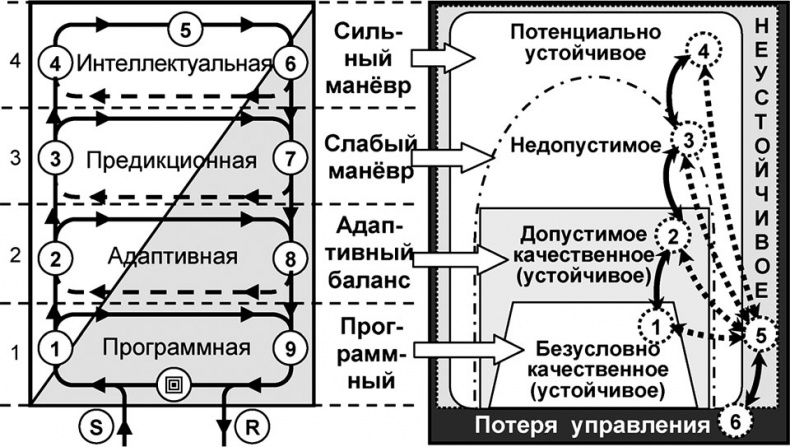
Рис. 6.14. Стандартные области устойчивость систем 4U
Очевидно, что высшие универсумные уровни (4) и (3) способны обеспечивать работу систем в режиме самоуправления и в них необходимо учитывается влияние положительной обратной связи, т. е. это – режим манёврирования. Уровням (2) и (1) более характерны исполнительские, стабилизирующие, пассивные функции, т. е. они работают под влиянием отрицательной обратной связи[173], в балансировочном режиме управления. Из этой стратификации легко вывести её соответствие ряду граничных состояний, представляющих следующую иерархию:
1) Безусловно качественное (классическое устойчивое) управление (цифра 1 в точечном круге) обеспечивается в области, где система управляется по закону однозначной ответной реакции на определенное входное воздействие. Пример: нажал водитель (СУ) на тормоз (ПС) – машина (ОУ) затормозила (ОС), повернул руль – машина осуществляет поворот. Это ни что иное, как алгоритмика работы программной схемы управления;



