Два комплекса одного и того же типа, составленные из однородных элементов-активностей, можно прямо сравнивать по их количественной устойчивости, не считаясь с конкретными воздействиями среды: если в комплексе А сумма элементов больше, чем в В, то эта его устойчивость во всяком случае соответственно больше при одних и тех же воздействиях, какие бы они ни были. …Напротив, о структурной устойчивости можно говорить всегда только по отношению к тем или иным воздействиям, а не по отношению ко всяким вообще; одному яду организм оказывает более значительное сопротивление, другому – более слабое и т. п.; для каждого разрушающего влияния коэффициент особый [7].
Рассмотрение любого объекта (ОЯП), как суперсистемы, стратифицированной в соответствии с универсумной логикой, позволяет выработать однозначные критерии расчёта его качественных показателей или, в традиционной и современной терминологии, степени его «прогрессивности», «инновационности», «креативности» и т. п.
6.5.2. Коэффициентирование категории «качество»
Самый распространённый пример перевода количественных характеристик в качественные – это запись чисел в разрядной сетке позиционных систем счисления. До определённого момента, зависящего от используемого основания системы счисления, позиция записи цифр не меняется. В десятичной системе цифры от 0 до 9 пишутся в одной и той же позиции. Но число 10 в десятичной системе уже нельзя записать в той же позиции. Для его записи требуется создание новой ячейки разрядной сетки, в которую теперь будут записываться не числовые «единицы», а качественно новые «десятки». Набор цифр будет тем же – от 0 до 9, но их «весовая» характеристика будет качественно другой. Третья позиция определит цифрам порядок «сотен», следующая – «тысяч» и т. д.
Порядковые изменения – это как раз то, что переводит количество в качество и наоборот. Запись цифры в старший разряд – это перевод в новое состояние следующей по иерархии весов ячейки числовой памяти.
По аналогии с записью чисел можно утверждать, что основание системы счисления и диапазон изменения параметров определяют количество стратификационных уровней. Для десятичной системы качественные кванты или «весовые страты» – это единицы, десятки, сотни, тысячи и т. д. Конечно же, модели реальных стратификаций могут быть значительно сложнее, ведь они должны учитывать разнообразные комбинаторные варианты взаимосвязей элементов на различных уровнях.
Расчёт количества информации по методу К. Шеннона при наступлении равновероятных событий (или, что эквивалентно, показатель степени для представления двоичного числа) выражается формулой
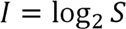
(6.1)
где
I – количество информации (или показатель степени числа S);
S – число равновероятных событий (или число S).
При стратификационном описании универсума формула практически не видоизменится
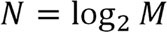
(6.2)
где
N – число универсумных страт.
M – число дискретных состояний универсума;
Проведём стратификационное коэффициентирование универсума. Общее число его дискретных состояний (исключая нулевой уровень)
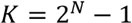
(6.3)
где
K – общее число дискретных состояний;
N – число универсумных страт.
Определим коэффициенты качества (или, что эквивалентно, весовые стратификационные коэффициенты) для U-элементов каждой старты
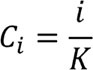
(6.4)
где
i – порядковый номер страты;
Ci – коэффициент качества i-ой страты.
Очевидно, что рис. 195
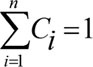
(6.5)
Если для количественного распределения по стратам универсумных элементов TC провести операцию нормировки
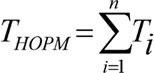
(6.6)
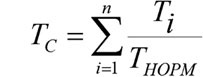
(6.7)
то наличие определённого нормированного количества элементов на стратах позволит получить уникальную качественную характеристику любого варианта распределения элементов по стратам
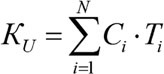
(6.8)
где
N – число универсумных страт;
Ci – коэффициент качества i-ой страты;
Ti – количество элементов (состояний) на i-ой страте.
Это порядок получения числовой «поэлеменно смешанной» информационно-материальной иерархии стратификационных коэффициентов, представляющий следующие ряды:
– для 2U: C1=0,33(3); C2=0,66(6);
– для 3U: C1=0,1429; C2=0,2857; C3=0,5714;
– для 4U: C1=0,06(6); C2=0,13(3); C3=0,26(6); C4=0,53(3) и т. д.
При таком коэффициентировании, например, коэффициент 0,33(3) говорит о том, что данная страта содержит соответствующую коэффициенту долю ИМ-компонентов.
Между тем, если речь ведётся преимущественно об информационном состоянии ОЯП, то алгоритм расчёта весовых характеристик качества объектов должен включать в себя статистику не столько элементного, сколько информационного трафика (величины информационного потока) этих элементов, то есть «долю» структурных связей (связок и/или ссылок) между элементами по каждой универсумной страте.
Реальный алгоритм коэффициентирования, рассматриваемый далее, должен использовать именно «информационную долю», причём долю относительную, характерную именно для своего стратификационного положения. После проведения расчёта получим следующие ряды:

