1. Спам-фильтры. Основная гипотеза: любое конкретное сообщение, приходящее по электронной почте, не спам. Ваш спам-фильтр отыскивает признаки, которые могут использоваться для отказа от нулевой гипотезы для того или иного конкретного сообщения, например огромные списки рассылки или наличие фраз типа «удлинение пениса». Ошибка первого рода предполагает отбраковку сообщения, которое на самом деле не является спамом («ложный позитив»). Ошибка второго рода предполагает пропуск спама через фильтр и его попадание в ваш почтовый ящик («ложный негатив»). Сравнивая последствия от потери важного сообщения и незначительное раздражение, вызванное получением совершенно не интересующего вас письма, содержащего, скажем, рекламу БАДов, большинство людей, скорее всего, предпочтут терпеть неудобства, обусловленные ошибками второго рода. Оптимально разработанный спам-фильтр должен требовать относительно высокой степени определенности, прежде чем отвергнуть нулевую гипотезу и заблокировать соответствующее сообщение.
2. Проверка на наличие раковых заболеваний. Существуют многочисленные тесты для раннего выявления раковых заболеваний, например маммография (рак молочной железы), ПСА-тест (рак простаты) и даже магнитно-резонансная визуализация (МРТ) всего тела для выявления всего, что может вызывать подозрения. Основная гипотеза для каждого, кто проходит такое обследование, заключается в том, что он не болен раком. Проверка на наличие раковых заболеваний используется для того, чтобы отвергнуть нулевую гипотезу, если результаты тестирования вызывают подозрения. Соответствующее предположение всегда исходит из того, что ошибка первого рода («ложный позитив», что в конечном счете означает отсутствие заболевания) безусловно предпочтительнее ошибки второго рода («ложный негатив», который означает, что диагностирование не выявило заболевания, которое на самом деле имеется). Проверка на наличие раковых заболеваний является полной противоположностью примеру со спам-фильтром. Врачи и пациенты готовы мириться с умеренным количеством ошибок первого рода («ложный позитив»), чтобы избежать вероятности появления ошибок второго рода («ложный негатив»), когда пациенту не диагностируется раковое заболевание, хотя в действительности он болен. Впрочем, в последнее время специалисты в области политики охраны здоровья подвергают сомнению такой подход из-за высоких издержек и побочных эффектов, связанных с «ложными позитивами».
3. Поимка террористов. В этой ситуации неприемлема ни ошибка первого, ни ошибка второго рода. Именно поэтому в обществе продолжаются дебаты, связанные с поиском подходящего баланса между борьбой с терроризмом и защитой гражданских прав. Основная гипотеза в данном случае заключается в том, что человек не террорист. Как и в обычном уголовном контексте, нам не хотелось бы совершать ошибки первого рода и отправлять невиновных в тюрьму Гуантанамо. Однако в мире, где накоплено большое количество оружия массового поражения, даже одного террориста опасно оставлять на свободе (ошибка второго рода), поскольку это может повлечь за собой поистине катастрофические последствия. Именно поэтому – нравится вам это или нет – власти Соединенных Штатов удерживают в Гуантанамо людей, подозреваемых в терроризме, основываясь при этом даже на меньшей доказательной базе, чем могло бы потребоваться для вынесения им обвинительного приговора в обычном уголовном суде.
Статистический вывод – это не волшебная палочка и отнюдь не безошибочный метод. Тем не менее это замечательный инструмент для осмысления мира. Мы можем глубже понять многие явления нашей жизни лишь путем нахождения им наиболее вероятного объяснения. Многие из нас делают это постоянно (например, мы говорим: «Мне кажется, этот молодой человек, развалившийся на полу в окружении множества пустых банок из-под пива, хватил лишку», а не «Мне кажется, что этого молодого человека, развалившегося на полу в окружении множества пустых банок из-под пива, отравили террористы»).
Статистический вывод лишь формализует процесс.
Приложение к главе 9
Вычисление стандартной ошибки для разности средних значений
Формула для сравнения двух средних значений
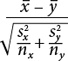
где x̅– среднее значение выборки x
y̅ – среднее значение выборки y
sx – среднеквадратическое отклонение выборки x
sy – среднеквадратическое отклонение выборки y
nx – количество наблюдений в выборке x
ny – количество наблюдений в выборке y
(В числителе вычисляется разность двух средних значений; в знаменателе – стандартная ошибка для разности двух средних значений разных выборок.)
Нулевая гипотеза: средние значения этих двух выборок одинаковы. Приведенная выше формула вычисляет наблюдаемую разность средних значений относительно величины стандартной ошибки для разности средних значений. Как и прежде, мы предполагаем, что имеем дело с нормальным распределением. Если средние значения исходной совокупности действительно одинаковы, то можно ожидать, что разность средних значений двух выборок окажется меньше одной стандартной ошибки в 68 случаях из 100 и меньше двух стандартных ошибок в 95 случаях из 100 (и т. д.).
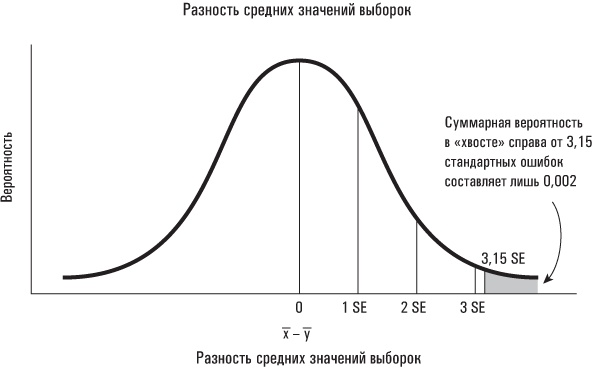
В приведенном примере с аутизмом разность средних значений двух выборок составляла 71,6 кубических сантиметра при стандартной ошибке 22,7. Отношение этой наблюдаемой разности равняется 3,15; это означает, что средние значения двух указанных выборок отстоят друг от друга более чем на три стандартные ошибки. Как уже отмечалось, вероятность получения выборок со столь различающимися средними значениями в случае, если средние значения исходных совокупностей одинаковы, чрезвычайно низкая. Точнее говоря, вероятность наблюдения разности средних значений, составляющей не менее 3,15 среднеквадратических ошибок, равняется 0,002.
Проверка гипотез с одно– и двусторонним критерием
Когда мы использовали пример со сравнением роста профессиональных баскетболистов с ростом мужского населения в целом, я сознательно упустил одну маленькую деталь. Наша нулевая гипотеза заключалась в том, что рост профессиональных баскетболистов такой же, как средний рост мужского населения в целом. Однако я не указал, что в действительности у нас есть две возможные альтернативные гипотезы.
Одна заключается в том, что средний рост профессиональных баскетболистов отличается от среднего роста мужского населения: они могут быть выше или ниже, чем другие мужчины в совокупности. Именно таким подходом вы воспользовались, когда проникли в автобус, угнанный террористами, и определили вес пассажиров, чтобы выяснить, являются ли они участниками исследования Americans’ Changing Lives. Вы могли отвергнуть нулевую гипотезу, что пассажиры угнанного автобуса являются участниками этого исследования, если бы их средний вес был значительно больше, чем средний вес участников исследования, или значительно меньше (как и оказалось на самом деле). Вторая альтернативная гипотеза заключается в том, что средний рост профессиональных баскетболистов превышает средний рост остального мужского населения. В этом случае нам пригодится обычный жизненный опыт, который подсказывает, что рост профессиональных баскетболистов не может быть меньше, чем средний рост остального мужского населения. Различие между этими двумя альтернативными гипотезами определяет, выполняем ли мы проверку гипотез с односторонним или двусторонним критерием.

