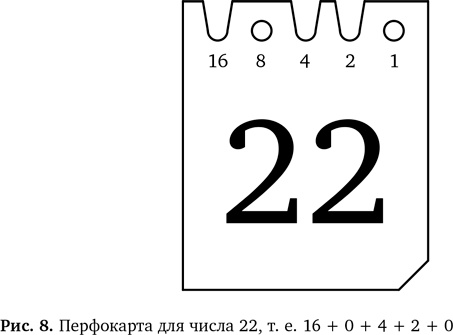
На рис. 8 приведен пример перфокарты для числа 22. Чтобы увидеть, как использовать перфокарты для поиска данных с помощью магического принципа «шиворот-навыворот», давайте сделаем их сами, а потом посмотрим, как они действуют.
Шаблоны для перфокарт можно скачать здесь: www.cs4fn.org/punchcards/.
Распечатайте их — в идеале прямо на тонком картоне — и слегка посыпьте тальком, чтобы они не склеивались (это важно).
Вместо отверстий и их отсутствия мы будем использовать в нашем коде отверстия и небольшие вырезы. Вам следует сделать вырезы в нужных местах, чтобы в сумме получилось число, крупно написанное на карте. Например, на карте 22 есть вырезы напротив 16, 4 и 2, а 16 + 4 + 2 = 22. Чтобы понять происходящее, нужно знать кое-что из простой математики, а именно двоичную систему счисления.
Две системы
Двоичный код — это способ записывать числа, при котором в нашем распоряжении 0 и 1 вместо 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, которыми мы обычно пользуемся. Наша обычная система называется десятичной. В двоичной системе всего два символа, и на перфокартах мы будем использовать круглые отверстия для 0 и щели для 1. Двоичная и десятичная системы — просто две разные системы представления чисел. Выбрать правильное представление информации — еще один важный элемент вычислительного мышления.
Давайте сначала рассмотрим десятичную систему и сравним ее с двоичной. В десятичной системе, чтобы досчитать до 9, мы используем цифры, но они заканчиваются, и в этот момент мы переходим в новый столбик. Мы возвращаемся к 0, но переносим 1 в следующий столбик, и 1 теперь обозначает 10, как показано на рис. 9.
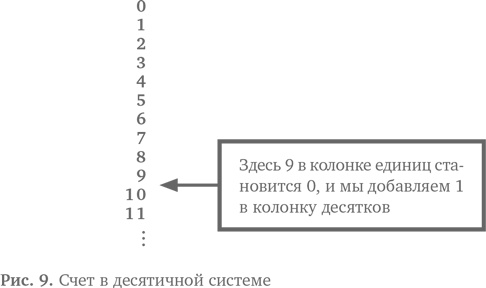
Любая цифра во втором столбике обозначает на 10 больше, чем та же цифра в первом столбике. В десятичной системе 16 — это один десяток (1 в столбике десятков) и шесть единиц (6 в столбике единиц). Мы добавляем 10 к 6, чтобы получить число 16. Подобным образом, 987 обозначает 9 раз по 100, 8 раз по 10 и 7 раз по одному, сложенные вместе.
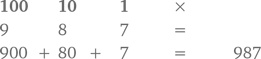
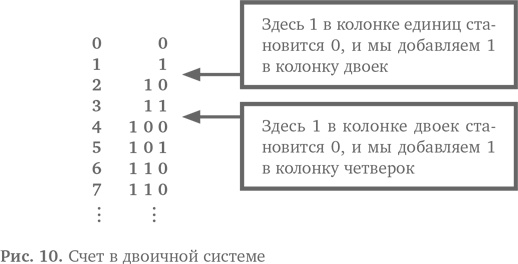
Двоичная система работает точно так же, только у нас раньше заканчиваются цифры. Дойдя до 1, мы уже переходим в новый столбик, до 9 нам не добраться (рис. 10). Это значит, что столбцы теперь предназначены для единиц, двоек, четверок, восьмерок и так далее — вместо единиц, десятков и сотен. То есть в двоичной системе (используя только 1 и 0) мы записываем, например, число 5 как 101. Это 1 в разряде четверок плюс 0 в разряде двоек и плюс 1 в разряде единиц.
Если распределить это на пять колонок (как мы сделаем это на перфокартах), то 5 в двоичной системе будет выглядеть как 00101.

Подобным образом, 16 в двоичной системе — это 10000.

Отметим, что, помимо колонки единиц, все остальные колонки обозначают степени двойки, то есть четные числа. Поэтому единственный способ представить нечетное число в двоичной системе — поставить 1 в колонку единиц. У всех нечетных чисел в ней будет 1, а у четных — 0. Насколько это важно, мы увидим ниже.
Двоичные перфокарты
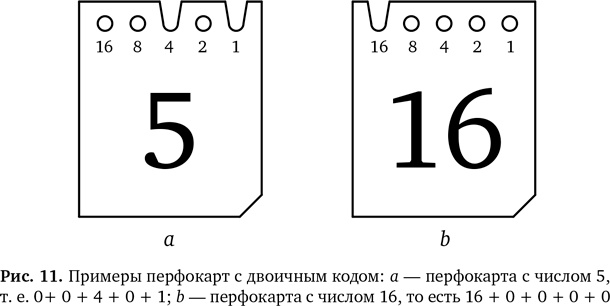
Какое отношения это имеет к нашим перфокартам? На них мы можем записывать числа в двоичной системе, используя отверстия для 0 и вырезы для 1. Чтобы записать на перфокарту число 5, начиная слева, нам нужно отверстие (0), еще отверстие (0), потом вырез (1), снова отверстие (0) и, наконец, вырез (1). Для числа 16 (10000) нам нужен один вырез и 4 отверстия. Если у нас есть место для пяти отверстий, мы можем записать на карту любое число до 31. Имея достаточно места (то есть достаточно степеней двойки и, соответственно, разрядов), мы можем записать любое число. Описанные примеры перфокарт приведены на рис. 11а и 11b.
Как только мы записали на карту число в двоичном коде в виде отверстий и вырезов, можно с легкостью найти любую карту. И здесь наступает черед метода «шиворот-навыворот».
Возьмите стопку карт и убедитесь, что они сложены срезанными уголками друг к другу, а отверстия выровнены в одну линию. Теперь вставьте карандаш в крайнее правое отверстие (колонку единиц) и стряхните все карты, у которых в этом месте вырез (как мы помним, это нечетные числа). У вас останутся только карты с 0. Теперь вернитесь к числу, которое вы хотите найти. Если в его двоичном коде в конце стоит 0, то сбросьте нижнюю стопку — те карты, которые вы стряхнули. Если в целевом числе там стоит 1, то оставьте нижнюю стопку. Повторите то же самое для каждого отверстия по очереди.
Например, мы ищем карту с номером 16. В двоичной системе это 10000. При движении слева направо выходит:
ВЫРЕЗ 1: 0 — СБРОСЬТЕ упавшие карты.
ВЫРЕЗ 2: 0 — СБРОСЬТЕ упавшие карты.
ВЫРЕЗ 4: 0 — СБРОСЬТЕ упавшие карты.
ВЫРЕЗ 8: 0 — СБРОСЬТЕ упавшие карты.
ВЫРЕЗ 16: 1 — ОСТАВЬТЕ упавшие карты.
Многократно сбрасывайте нижнюю стопку, пока, в пятом раунде, ее не нужно будет оставить. У вас останется карта с номером 16. Таким образом, прорабатывая двоичный код, можно найти любую карту. Попробуйте найти карту 5. В двоичной системе это 00101. При движении справа налево получаем:
ВЫРЕЗ 1: 1 — ОСТАВЬТЕ упавшие карты.
ВЫРЕЗ 2: 0 — СБРОСЬТЕ упавшие карты.
ВЫРЕЗ 4: 1 — ОСТАВЬТЕ упавшие карты.
ВЫРЕЗ 8: 0 — СБРОСЬТЕ упавшие карты.
ВЫРЕЗ 16: 0 — СБРОСЬТЕ упавшие карты.
У вас останется карта 5.
Как же это работает?
Оказывается, сбрасывая карты таким образом, вы поступаете как фокусник, сдающий карты по принципу «шиворот-навыворот». Чтобы это увидеть, нужно снова подключить логическое мышление и с его помощью найти точное объяснение происходящему.

