Я могу помочь. Всего за две монеты я могу найти в колоде твою уникальную карту. Если носить ее с собой, она будет символизировать и указывать дорогу, которая приведет к гармонии и принесет удачу.
Я чувствую твои сомнения. Я должна подтвердить, что слияние энергий произошло и что контакт установлен в нужной мере. Чтобы это проверить, тебе необходимо добровольно выбрать карту из колоды. Если цвета карт, выбранных тобой и мной, совпадут, это подтвердит контакт. Если я потерплю неудачу, то заплачу тебе неустойку. Ты получишь назад три монеты — одной я искуплю прискорбную ошибку в моем предсказании.
Хочешь, чтобы карты показали будущее? Ты точно ничего не потеряешь и, возможно, многое приобретешь!»
Сеанс заканчивается… дважды
Первый вариант: вы платите две монеты, предсказательница выбирает удачную карту, а потом вы берете случайную карту из колоды. Цвета совпадают — обе карты красные. Контакт есть. Затем вам предсказывают будущее по картам, и вы выходите из комнаты, а предсказательница, явно утомленная соединением нитей судьбы, кладет монеты в карман и тихо покидает комнату.
Второй вариант: вы платите две монеты, вам показывают удачную карту, вы выбираете вторую, но, к сожалению, цвета не совпадают — выпали красная и черная. Обещанный контакт не подтвержден. Предсказательница приносит извинения: тонкий план сегодня рассинхронизирован. Вам дают обещанные три монеты — две ваших и еще одну в качестве компенсации за разочарование. Гадалка извиняется. Возможно, получится в следующий раз, но и сейчас вы скорее приобрели, чем потеряли. Выходя из комнаты, вы богаче, чем были, когда вошли. И, может быть, уже подумываете зайти в другой раз, когда знамения будут благоприятными.
Каким бы ни был финал, все это — мошенничество с целью наживы, но как оно работает? С виду все честно. Но почему люди ловятся на такие схемы в реальности?
Схема аферы
В чем же обман? Давайте посмотрим, как загадочная математика превращает вроде бы честную схему в принципиально мошенническую. За аферой стоит простая математическая ошибка, которую делают люди, чью бдительность усыпили образ предсказательницы и сценарий диалога (подробнее о нем ниже). Посмотрим на математическую подоплеку. Если наша искусственная гадалка выбирает удачную карту нужного цвета, ей достаются две монеты. Если у нее не получается, она платит три монеты. Этот штраф кажется приличным вознаграждением, пока вы не вспоминаете, что две из этих монет вы сами отдали за предсказание. Таким образом, если карты не совпадают, ИИ теряет только одну монету.
Здравый смысл подсказывает, что нужно рассмотреть вероятность обоих исходов. Удачная карта, по сути, ерунда, это просто любая карта, взятая из полной колоды. Тестовая карта — еще одна случайная карта из оставшейся колоды. То есть это все равно что играть в цветной «Снап!» с полной перетасованной колодой. Шанс, что две карты совпадут по цвету (выпадут черная с черной или красная с красной), равен шансу, что карты не совпадут по цвету (выпадут красная с черной или черная с красной). Это шанс 50 : 50.
Если наш ИИ-псевдогадалка повторит эту схему несколько раз, то начнет получать деньги. Почему? Представьте, что у него появится 10 жертв. В среднем, сыграв 10 раз, 50% (пять человек) отыграют деньги, потому что карты не совпадут, однако 50% (пять человек) уйдут без наличности. На рис. 53 эта ситуация обобщена.
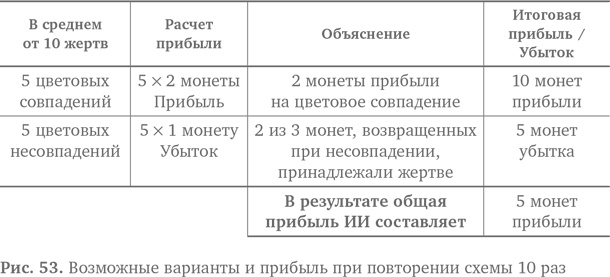
Чем больше людей сыграет, тем больше сможет получить мошенник-ИИ. Сделать ошибку довольно легко. Мы не видим, какие математические последствия повлекут наши действия в долгосрочной перспективе. Такие вещи происходят часто, и не только в случае мошенничества. Например, парадокс дня рождения: как это ни удивительно, если в одном помещении соберутся всего лишь 23 человека, шанс, что у двоих совпадет день рождения, равен 50%.
Поймаем их на Барнума
Теперь мы знаем, как устроена наша мошенническая схема. Но как заставить людей на нее купиться? Если не вдаваться в подробности, хватит убедительной математики. Если нечего терять, значит, нет причин не вступить в игру. Но есть и другие способы, которые помогут нам привлечь клиентов. В шестой главе мы говорили о виртуальном собеседнике— это системы ИИ, способные имитировать разговор. Они работают в беседах на общие темы, но можно ли создать с их помощью интерфейс для взаимодействия с клиентом, который будет таким же убедительным, как гадалка?
У нас должно сразу сложиться впечатление, что виртуальный собеседник умеет предсказывать, — еще до того, как он предложит вытащить удачную карту. Но как псевдогадалке завоевать доверие? Для этого пригодятся так называемые утверждения Барнума, которые применяют, чтобы вызвать доверие, манипулируя нашим восприятием языка. Они названы в честь знаменитого циркового антрепренера Финеаса Барнума,который прославился своими мистификациями. Эффект Барнума основан на том, что люди склонны видеть точное описания себя в утверждениях, которые на самом деле применимы к большим группам, например «порой вы сомневаетесь в сделанном выборе» или «некоторые ваши сны очень далеки от реальности». Да уж! Конечно, они подходят всем, но в ходе экспериментов участники указывали, что именно эти утверждения относятся непосредственно к ним. Диалог с нашей ИИ-гадалкой с самого начала строится с использованием утверждений Барнума. То есть в разговоре фигурируют только обобщения, но мы обрабатываем их смысл таким образом, что нам кажется, будто ИИ обладает неким глубоким и мистическим знанием о нас. Так нас втягивают в аферу со счастливой картой.
Как и любой виртуальный собеседник, наш тоже может вести более сложный диалог. Необязательно следовать точному сценарию. Можно на выбор взять набор утверждений Барнума. Это может быть случайный выбор, или же робот будет реагировать на высказывания жертвы с помощью наиболее подходящих утверждений Барнума, и тогда получится убедительнее. Вы, как создатель, сами определяете уровень сложности.
Строим шаг за шагом
Итак, у нас есть убедительная мошенническая схема и бот, который будет привлекать игроков и заставлять их расставаться с деньгами. Чтобы создать ИИ, который сможет целиком провернуть эту аферу, необходимы еще два элемента. Система должна проверять, действительно ли игрок отдал деньги. В противном случае может выясниться, что она сама стала жертвой обмана — радостно раздавала деньги, но ничего не брала себе! Ей нужно уметь проверять, положила ли жертва две монеты на стол. Но этот элемент мы уже создали — мы просто возьмем одну обученную нейронную сеть из главы 7.
Кроме того, нам нужно, чтобы она понимала, когда брать деньги, а когда платить. Для этого она должна проверять, действительно ли две выбранные карты одного цвета. Этот элемент мы тоже уже создали! Нам потребуется другая нейронная сеть из главы 7 — та, которая умеет играть в цветной «Снап!».
Вот так, объединив старые и модифицированные компоненты, мы сделаем робота-мошенника. Это обычный чат-бот, работающий с утверждениями Барнума, наш счетчик монет, обученный необходимым действиям, и система, играющая в «Снап!», — только она не будет кричать «Снап!», а займется проверкой карт.



