Для этих изображений мы выбираем одну из всего двух цифр на каждый пиксел — 1 или 0, поэтому у нас всего два цвета, белый и черный. Если использовать больше цифр, где каждая будет представлять свой цвет, то можно подобным образом сохранять цветные изображения.
Альтернативное представление изображения — сохранить его в виде линий и фигур, из которых оно состоит. Это так называемые векторные методы. Мы определяем начальные и конечные точки для тысяч линий и быстро рисуем их на экране. Например, чтобы нарисовать квадрат, вместо обозначения каждого пиксела в сетке вы сохраняете серию инструкций:
Линия (Север, 50)
Линия (Восток, 50)
Линия (Юг, 50)
Линия (Запад, 50)
Чтобы нарисовать изображение, мы просто выполняем инструкции. Такое представление в целом занимает гораздо меньше места, но у него есть еще одно большое преимущество. Инструкция выше позволяет нарисовать квадрат со стороной 50. Допустим, мы хотим получить изображение в 10 раз больше. В этом случае просто умножаем все значения на 10. Если же мы хотим, чтобы квадрат был в 10 раз меньше, то делим их на 10. Благодаря этому представлению мы можем увеличить изображение до любого размера, например чтобы показать его на большом экране, но без необходимости хранить еще больше данных и не теряя точности.
Вот почему представление диаграмм как в pdf-файлах занимает меньше места и выглядит одинаково хорошо, как бы вы ни увеличивали изображение. В таких файлах хранятся векторные версии. Изображение в формате jpeg требует больше памяти, чтобы сохранить картинку в более высоком разрешении, и при сохранении нужно указать, каким именно оно будет. Вот почему, приближая изображение в формате jpeg, вы видите, что все расплывается и линии становятся неровными.
С помощью векторных методов мы создаем трехмерные формы, объединяя много, порой десятки тысяч, так называемых графических примитивов — сфер, кубов, цилиндров и так далее. Различные комбинации позволяют нам создавать желаемые сложные формы.
Существуют системы, которые симулируют распределение световых лучей в искусственном мире (для этого требуется компьютерное моделирование — на сей раз чтобы показать, как источники света освещают предметы). С их помощью создают фотореалистичные изображения. Кроме того, к нашим графическим примитивам добавляют скрипты, отвечающие за сложные движения персонажей, — их часто создают, снимая движения настоящих актеров, — и таким образом фигуры будут двигаться как мы хотим. Ограничения — это объем доступных вычислительных мощностей, качество кода, который пишут кодировщики-программисты, чтобы графика выглядела еще естественнее, и воображение творческого человеческого разума. Но даже простая сетка и несложные правила кодирования могут дать замечательные результаты.
Жизнь как игра
Играем в сетке
Давайте начнем с простого — с игры, в которой есть квадратная сетка и набор правил, в зависимости от которых на ней появляются и исчезают пикселы. Значение пиксела меняется и зависит от того, сколько других пикселов находится рядом. Звучит не очень интересно, правда? Но не торопитесь с выводами. Даже в этой простой игре происходит много интересного, и мы используем ее, чтобы кое-что понять о мире природы.
Игра называется «Жизнь», ее автор — математик Джон Конвей. Впервые правила игры были опубликованы в 1970 г., и впоследствии она приобрела популярность у программистов по всему миру. Правила просты, хотя Конвей приложил массу усилий, чтобы их правильно сбалансировать и гарантировать интересный игровой процесс.
Сетка представляет собой небольшой квадратный мир с клетками (пикселами), которые могут присутствовать (быть живыми) и отсутствовать (быть мертвыми). У каждой клетки есть окружение из восьми других, которые непосредственно прилегают к ней по горизонтали, вертикали и диагонали. Чтобы выжить, существующая живая клетка должна иметь два или три живых соседа — этого достаточно для поддержания жизни, но не слишком много. Если у любой живой клетки окажется менее двух соседних, она умрет из-за недостаточной населенности. Подобным образом любая живая клетка, у которой более трех живых соседей, умрет от перенаселения. Наконец, каждая живая клетка, у которой есть три живых соседа, активизируется и имитирует процесс размножения. Эти принципы обобщены в порождающих правилах на рис. 55.

На рис. 56 показан пример такой модели и один жизненный цикл.
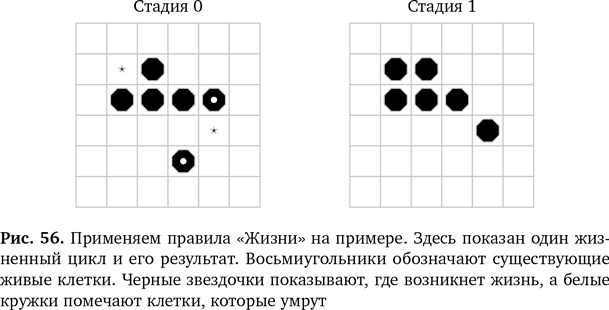
Благодаря этой простой математике и простому набору порождающих правил, которые применяются к клеткам на сетке, на игровом поле возникают странные и интересные модели, которые с течением времени меняются. Клетки живут и умирают по заданным правилам.
Сыграйте сами
Вы можете сыграть в эту игру самостоятельно. Для этого понадобится большая сетка. Для начала сгодится шахматная доска, но вы скоро осознаете, что нужно больше пространства. Больше подойдет доска для игры в го, если она у вас найдется. Как вариант, можно нарисовать большую сетку на самом большом листе бумаги, какой вы только найдете. В идеале лист должен быть бесконечным, но тогда он не поместится в вашу спальню… поэтому придется принять, что, если игра дойдет до края доски, нужно будет быстро найти еще место либо признать, что это конец «Жизни» и все ваши существа упадут с края «вселенной».
Необходимо как-то помечать рождающиеся клетки. Полезно также выделять те, которые в следующем раунде умрут. Убирать их нельзя — они нужны, чтобы просчитать все изменения. К примеру, можно взять камни для игры в го — замените черные на белые, чтобы показать, какие клетки скоро умрут (и отправятся на небо). Еще вам понадобится как-то помечать квадраты, в которых зародится жизнь. Для этого используйте более мелкие предметы (например, бусины) другого цвета. Можно использовать три вида монет или цветных бусин (но, если в вашем мире закипит жизнь, их понадобится очень много).
Теперь остается только произвольно разместить фишки на доске, а потом рабски следовать законам «Жизни». В вашем мире это эквиваленты физических законов. Сначала определите все рождения и смерти, заменив фишки на новые на всей доске, а потом уберите умирающие клетки и замените живые на новорожденные, чтобы подготовиться к следующему раунду. Чтобы играть в «Жизнь», нужно уделять много внимания деталям. Если вы сделаете ошибку с одной клеткой, у вас получится совершенно другой расклад.
В интернете вы найдете самые разные симуляции и с их помощью увидите, как развивается жизнь в более крупных масштабах. Конечно, если вы умеете программировать, то попробуйте создать собственный вариант. В систему Turtle («Черепаха»), разработанную в Оксфордском университете (www.turtle.ox.ac.uk), входит программа игры «Жизнь», которая может послужить образцом.

