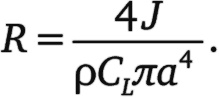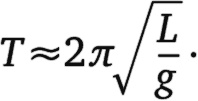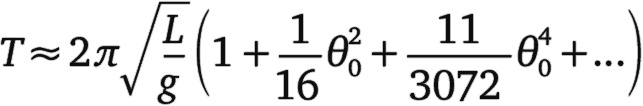J, момент инерции бумеранга. Он характеризует то, насколько трудно закрутить бумеранг; чем тяжелее бумеранг, тем больше J. Момент инерции также зависит от формы бумеранга;
ρ, плотность воздуха, в котором летит бумеранг;
CL, коэффициент подъемной силы, – число, определяющее подъемную силу, действующую на бумеранг. Зависит от его формы;
π, число 3,14159…;
а, радиус бумеранга.
Радиус траектории бумеранга R определяется перемешиванием данных ингредиентов по следующему рецепту:
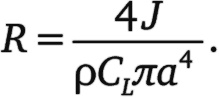
Из этого уравнения мы видим, что радиус траектории бумеранга не изменится, если мы будем бросать его сильнее, потому что скорость не входит в число ингредиентов приведенного рецепта
[19]. Но что произойдет, если мы сделаем бумеранг тяжелее, прилепив какое-то количество клейкой массы к концам его плеч-крыльев? Уравнение позволяет нам предсказать, что утяжеление массы увеличит момент инерции J, что, в свою очередь, приведет к возрастанию радиуса R. Итак, более тяжелый бумеранг будет лететь по окружности большего радиуса. Это полезно знать при запуске бумерангов в ограниченном пространстве!
С веб-сайта «Тайн 4исел» вы можете загрузить PDF-файл с инструкциями по изготовлению бумеранга.
Как заставить яйцо бросить вызов гравитации?
Возьмите яйцо, сваренное вкрутую. Положите его на стол и приведите во вращение. Яйцо примет вертикальное положение, словно бросая вызов законам гравитации. Не менее удивительно и то, что этот фокус не удастся с сырым яйцом.
Лишь в 2002 г. математики нашли объяснение этого поведения. Энергия вращательного движения преобразуется под действием силы трения поверхности стола в потенциальную энергию, и центр тяжести яйца приподнимается. Если у стола слишком малое либо слишком большое трение, то такого не произойдет. У сырого яйца часть вращательной энергии поглощается жидким содержимым, и остается недостаточно энергии для приподнимания центра тяжести.
Почему маятники не столь предсказуемы, как может показаться на первый взгляд?
И снова Галилео Галилей, мастер применения математики в целях предсказаний, первым раскрыл секрет движения маятника.
Как говорят, в возрасте семнадцати лет он присутствовал на мессе в кафедральном соборе Пизы. Галилей заскучал и стал разглядывать потолок, а потом его внимание привлекла люстра, которая плавно раскачивалась из-за ветра, гулявшего по зданию.
Галилей решил определить время, за которое люстра совершала колебание из стороны в сторону. У него не было наручных или карманных часов (они еще не были изобретены), поэтому он решил измерять время с помощью своего пульса. Великое открытие, совершенное Галилеем, состояло в том, что время колебания существенно не зависело от его размаха. Другими словами, время колебания существенно не изменится, если вы увеличите или уменьшите максимальный угол отклонения. (Я использовал слово «существенно» для указания на то, что при более тщательном исследовании положение вещей несколько усложнится.) Когда ветер дул сильнее, люстра описывала бо́льшую дугу, но на колебание уходило то же самое время, как и в случае, когда ветер ослабевал и люстра еле двигалась.
Это открытие было крайне важным, его результатом стало применение качающегося маятника для измерения времени. Когда вы даете ход маятниковым часам, не нужно беспокоиться о том, насколько далеко в сторону вы отводите маятник, особенно если учесть, что размах колебаний уменьшится с течением времени. Но от чего же зависит время совершения одного полного колебания, называемое периодом колебаний? Как изменится период колебаний, если увеличится масса либо возрастет длина маятника?
Как мы можем догадаться по экспериментам Галилея на Пизанской башне, более тяжелый маятник не будет перемещаться быстрее, поэтому период колебаний маятника не будет зависеть от его массы. В противоположность этому, увеличение длины маятника оказывает влияние на период колебаний. Он удваивается при увеличении длины в четыре раза. Увеличьте длину в 9 раз, и период утроится; если длина возрастет в 16 раз, период станет в четыре раза больше.
Опять-таки это предсказание можно отобразить с помощью уравнения. Период колебаний T возрастает прямо пропорционально квадратному корню из длины маятника L:
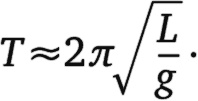
По существу, это другой способ написания уравнения, составленного Галилеем для мячей, падающих с Пизанской башни: g снова обозначает ускорение, обусловленное гравитацией. Причина написания знака приближенного равенства ≈ в противоположность знаку равенства = и моего предыдущего употребления слова «существенно» состоит в том, что данное выражение является хорошим приближением для периода колебаний. Пока размах колебаний не слишком большой, данной формулой можно пользоваться для предсказания поведения маятника. Но, если максимальный угол отклонения становится большим – например, маятник начинает движение почти из вертикального положения, – математика становится заметно сложнее. Теперь максимальный угол отклонения начинает оказывать влияние на период колебаний, чего Галилей не заметил, потому что люстра в кафедральном соборе не могла отклоняться настолько сильно. Мы также не наблюдаем данный эффект в напольных часах, потому что размах колебаний их маятника довольно мал.
Математика, необходимая для вывода уравнения, правильно предсказывающего поведение маятника с большим углом колебания, заметно выходит за пределы школьной программы. Ниже приведено начало этой формулы. На самом деле у нее бесконечное число слагаемых, которые вносят вклад в поведение маятника. θ0 – это выраженный в радианах начальный угол, образуемый маятником с вертикалью.
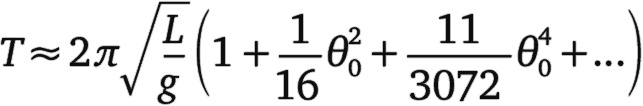
Но это ничто по сравнению с задачей предсказания поведения слегка модифицированного маятника. Вместо одного жесткого стержня, раскачивающегося вправо-влево, представьте, что к нижней части первого маятника шарнирным образом прикреплен второй. Поэтому конструкция в целом несколько напоминает ногу, верхняя и нижняя части которой соединяются в колене. Предсказать поведение этого двойного маятника крайне трудно. И дело не в том, что уравнения становятся существенно сложнее, а в том, что их решения крайне непредсказуемы: результат может быть совсем другим при ничтожном изменении начального положения маятника. Двойной маятник служит ярким примером математического явления, называемого хаосом. Но двойной маятник – не просто забавная настольная игрушка. Математика, лежащая в основе его поведения, имеет важные последствия для ответа на вопрос, который может повлиять на будущее всего человечества.