Эта серия примеров на простых формах демонстрирует мощь симметрии. Если мы знаем, что объект обладает симметрией, мы можем сделать вывод относительно некоторых его свойств. Если мы знаем, что набор объектов обладает симметрией, то на основании знания одного объекта мы можем сделать вывод о существовании и свойствах других. И если мы знаем, что законы природы обладают симметрией, то на основании знаний об одном объекте мы можем сделать вывод о существовании, свойствах и поведении новых объектов.
В современной физике симметрия позволяет предсказывать существование новых форм материи и формулировать новые, более всеобъемлющие законы. Например, специальную теорию относительности можно рассматривать в качестве постулата симметрии. Она говорит нам о том, что уравнения физики должны выглядеть по-прежнему, если мы преобразуем все объекты в этих уравнениях, добавив постоянную величину к их скоростям. Эта величина переносит один мир в другой, движущийся относительно него с постоянной скоростью. Специальная теория относительности говорит, что это отличие не дает различия — поведение в обоих мирах описывается одними и теми же уравнениями.
Несмотря на то что детали являются более сложными, процедуры использования симметрии для понимания нашего мира в основном соответствуют тем, которые мы использовали в нашем простом примере из мира треугольников. Мы считаем, что наши уравнения могут быть преобразованы таким образом, чтобы они в принципе изменились, и после этого мы требуем, чтобы они фактически не менялись. Возможное отличие не имеет никакого значения. Как и в примерах с треугольниками, для обеспечения общей симметрии должны соблюдаться несколько правил. Объекты, которые присутствуют в уравнениях, должны иметь особые свойства, образовывать связанные наборы и подчиняться тесно связанным законам.
Таким образом, симметрия может быть мощной идеей с богатыми следствиями. Кроме того, эту идею очень любит Природа. Приготовьтесь к публичной демонстрации любви.
Гайки, болты, катушки и палочки
Теория кварков и глюонов называется квантовой хромодинамикой или КХД. Уравнения КХД приведены на рис. 7.3
[17].
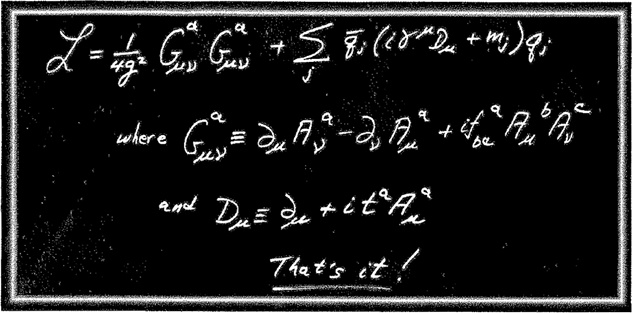
Рис. 7.3. Приведенный здесь лагранжиан L для КХД в принципе представляет собой полное описание сильного взаимодействия. Здесь mj и qj — это масса и квантовое поле кварка сорта j, а A — это глюонное поле с пространственно-временными индексами μ,
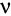 и цветовыми индексами а, b, c. Значения числовых коэффициентов ƒ и t полностью определяются цветовой симметрией. Помимо масс кварков, константа взаимодействия g является единственным свободным параметром в теории. На практике, чтобы вычислить что-либо с помощью лагранжиана L, требуются немалая изобретательность и упорный труд
и цветовыми индексами а, b, c. Значения числовых коэффициентов ƒ и t полностью определяются цветовой симметрией. Помимо масс кварков, константа взаимодействия g является единственным свободным параметром в теории. На практике, чтобы вычислить что-либо с помощью лагранжиана L, требуются немалая изобретательность и упорный труд
Довольно компактно, не правда ли? Ядерная физика, новые частицы, странное поведение, происхождение массы — все здесь!
На самом деле вам не стоит сразу удивляться тому факту, что мы можем записать уравнения в компактной форме. Наш умный друг Фейнман показал, как записать уравнение Вселенной в одну строку. Вот оно:
U = 0.
U — это определенная математическая функция, выражающая все. Это сумма вкладов всех частичных законов физики. Чтобы быть точным, U = UНьютон + UЭйнштейн + … Например, вклад ньютоновской механики UНьютон определяется как UНьютон = (F – ma)2; вклад эйнштейновского соотношения «масса/энергия» определяется как UЭйнштейн = (Е – mc2)2 и т.д. Поскольку каждый вклад положителен или равен нулю, то единственный способ обращения U в ноль подразумевает обращение в ноль каждого вклада. Поэтому выражение U = 0 подразумевает то, что F = ma, E = mc2, и это касается любого другого прошлого или будущего закона!
Так мы можем охватить все известные нам законы физики и учесть еще не открытые в одном универсальном уравнении. Теория Всего!!! Разумеется, это жульничество, поскольку не существует никакого способа использовать или даже определить U, кроме разбиения на отдельные фрагменты и их дальнейшего применения.
Уравнения, приведенные на рис. 7.3, очень сильно отличаются от шуточной унификации Фейнмана. Как и в U = 0, в управляющих уравнениях КХД зашифровано множество отдельных более мелких уравнений. (Для экспертов: управляющие уравнения содержат матрицы тензоров и спиноров, более мелких уравнений, компоненты которых включают обычные числа.) Тем не менее существует большая разница. Когда мы раскладываем уравнение U = 0, мы получаем множество не связанных друг с другом вещей. Когда мы раскладываем управляющие уравнения КХД, мы получаем уравнения, которые связаны симметрией — цветов, различных направлений в пространстве, а также симметрией специальной теории относительности между системами, движущимися с постоянной скоростью. Все их содержимое непосредственно доступно, а распаковывающие их алгоритмы вытекают из однозначной математики симметрии. Итак, позвольте мне заверить вас в том, что вы сейчас действительно удивитесь! Это по-настоящему элегантная теория.
Данная элегантность проявляется, в частности, в том, что суть КХД можно без серьезного искажения отразить в нескольких простых картинках. Они приведены на рис. 7.5. Мы обсудим их прямо сейчас.
Но сначала в качестве разминки и для сравнения я хотел бы в аналогичном формате представить суть квантовой электродинамики (КЭД). Как следует из названия, КЭД предполагает квантово-механическое описание электродинамики. Теория КЭД несколько старше теории КХД. Основные уравнения квантовой электродинамики были сформулированы уже к 1931 году, однако на протяжении долгого времени люди совершали ошибки при попытке их решения и получали бессмысленные (бесконечные) ответы, из-за чего эти уравнения получили плохую репутацию. И только около 1950 года несколько блестящих теоретиков (Ханс Бете, Синъитиро Томонага, Джулиан Швингер, Ричард Фейнман, Фримен Дайсон) решили проблему.
Суть КЭД можно выразить с помощью единственного изображения, приведенного на рис. 7.4, а. На нем показано, что фотон реагирует на присутствие или движение электрического заряда. Эта маленькая картинка, хоть и кажется мультяшной, представляет собой гораздо больше, чем метафору. Это базовый процесс системного метода решения уравнений квантовой электродинамики, которым мы обязаны Фейнману. (Да, опять он. Прости, Мюррей.) Диаграммы Фейнмана изображают процессы в пространстве и времени, в результате которых частицы находившиеся в некотором месте в одно время, перемещаются в другое место в некоторое другое время. Между этими моментами они могут влиять друг на друга.



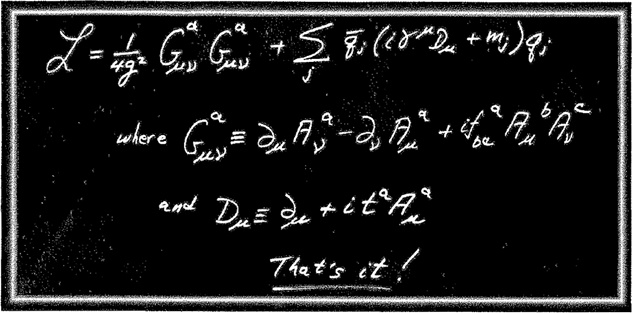
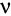 и цветовыми индексами а, b, c. Значения числовых коэффициентов ƒ и t полностью определяются цветовой симметрией. Помимо масс кварков, константа взаимодействия g является единственным свободным параметром в теории. На практике, чтобы вычислить что-либо с помощью лагранжиана L, требуются немалая изобретательность и упорный труд
и цветовыми индексами а, b, c. Значения числовых коэффициентов ƒ и t полностью определяются цветовой симметрией. Помимо масс кварков, константа взаимодействия g является единственным свободным параметром в теории. На практике, чтобы вычислить что-либо с помощью лагранжиана L, требуются немалая изобретательность и упорный труд