Наши глаза не приспособлены для разрешения расстояний порядка 10–14 сантиметров, а наш мозг не воспринимает временные промежутки порядка 10–24 секунд. Эти возможности не помогли бы нам спастись от хищников или найти брачных партнеров. Однако в результате просчета конфигураций Сетки наши компьютеры создают узоры, которые мы бы увидели, если бы наши глаза были способны воспринимать крошечные отрезки расстояния и времени. С помощью этих узоров мы можем заострить свое зрение. Именно это позволяет нам создать схему, изображенную на рис. 8.3.
После того как мы заставили «пустое» пространство «загудеть», мы можем его «пощипать». То есть обеспечить возмущение Сетки, добавив некоторую дополнительную активность, а затем позволить восстановиться покою. Если мы найдем стабильные, локализованные концентрации энергии, то это будет означать, что мы обнаружили — то есть вычислили — стабильные частицы. Мы можем сопоставить их (если эта теории правильна!) с протонами р, нейтронами n и т.д. Если мы находим локализованные концентрации энергии, которые сохраняются в течение довольно долгого времени, прежде чем рассеяться, это будет означать, что мы обнаружили нестабильные частицы. Они должны соответствовать
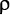 -мезонам (ро-мезонам), Δ-барионам (дельта-барионам) и их сородичам.
-мезонам (ро-мезонам), Δ-барионам (дельта-барионам) и их сородичам.
В этом состоит наше глубочайшее понимание того, что собой представляют р, n,
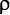 , Δ и другие частицы.
, Δ и другие частицы.
На рис. 9.1 показана конкретная задача, которая стоит перед нами. Это часть спектра адронов, то есть сильно взаимодействующих частиц, которые мы наблюдали. Они сопровождаются значениями двух ключевых определяющих свойств: массы и спина. Надпись содержит техническое описание изображенных объектов. Эти данные (а есть еще намного больше!) могут быть понятны специалистам, однако смысл в том, что существует множество интересных фактов, которые теории предстоит объяснить.
Далее, на рис. 9.2 показано, как три массы из измеренных используются для определения параметров теории. То есть до выполнения расчетов мы не знаем, какие массы мы должны присвоить кваркам или совокупной константе связи. Наиболее точным способом определения этих значений является сам расчет. Поэтому мы пробуем разные значения и останавливаемся на тех, которые лучше всего соответствуют наблюдениям.
Рис. 9.1. Перечень сильно взаимодействующих частиц, которые должны учитываться КХД. Каждая точка соответствует наблюдаемой частице. Высота точки показывает массу частиц. Первые два столбца — это мезоны со спином 0: π, K и спином 1:
 , K*,
, K*,
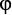 . Третий и четвертый столбцы — это барионы со спином 1/2: N, K; и спином 2/3: Δ, Ω соответственно. Пятый и шестой столбцы — это мезоны чармоний и боттомоний с различными спинами. Эти мезоны интерпретируются как связанные состояния тяжелого (очарованного) кварка с и его антикварка или соответственно (нижнего) кварка b и его антикварка. В этих столбцах высоты представляют собой массовые различия между частицей, о которой идет речь, и легчайшим состоянием чармония или боттомония
. Третий и четвертый столбцы — это барионы со спином 1/2: N, K; и спином 2/3: Δ, Ω соответственно. Пятый и шестой столбцы — это мезоны чармоний и боттомоний с различными спинами. Эти мезоны интерпретируются как связанные состояния тяжелого (очарованного) кварка с и его антикварка или соответственно (нижнего) кварка b и его антикварка. В этих столбцах высоты представляют собой массовые различия между частицей, о которой идет речь, и легчайшим состоянием чармония или боттомония
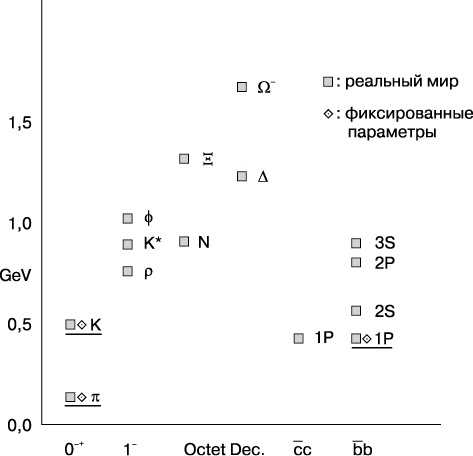
Рис. 9.2. Три массы используются для определения свободных параметров КХД. Таким образом, мы подгоняем, а не прогнозируем эти три массы. Однако после того, как мы это сделали, у нас больше нет места для маневра
Если теория имеет много параметров, вы регулируете их значения так, чтобы вместить как можно больше данных, таким образом, ваша теория не прогнозирует эти значения, а просто приспосабливает их. Для описания подобной деятельности ученые используют такие термины, как «аппроксимация кривой» и «подгоночные параметры». Эти фразы не являются лестными. С другой стороны, если теория включает лишь несколько параметров, но применяется к большому количеству данных, то она является очень мощной. Вы можете использовать небольшое подмножество измерений для определения параметров; в этом случае все остальные измерения будут предсказаны.
В этом объективном смысле КХД является очень мощной теорией. Мало того, что она не требует большого количества параметров, она их не допускает: только масса для каждого вида кварков и одна универсальная константа связи. Кроме того, большинство масс кварков не имеют значения для вычисления массы представленных на рисунке частиц с доступной нам степенью точности: другие эффекты вносят большую неопределенность. Нам нужна только средняя масса mlight самых легких кварков u и d, масса ms странного кварка и константа связи. После фиксации этих трех параметров у нас больше не будет возможностей для маневра. Надстроечные параметры отсутствуют, никакие оправдания не помогут, спрятаться негде. Если теория верна, то расчет будет соответствовать реальности. Если расчет не соответствует реальности, теория неверна.
На рис. 9.3 показано, как расчетные значения массы и спина — недвусмысленные предсказания КХД — соотносятся с наблюдаемыми значениями. Поскольку спин является дискретной величиной, мы имеем либо точное соответствие, либо разногласие. Таким образом, лучше бы мы обнаружили частицы с точно предсказанными спинами и приблизительно предсказанными массами. Со вздохом облегчения отмечаем, что возле каждого «реального» квадрата есть либо «вычисленный» круг, либо «фиксированный параметр» — ромб. Вы видите, что расчетные массы достаточно хорошо согласуются с наблюдаемыми значениями. Вокруг расчетных значений вы заметите вертикальные отрезки, соответствующие величине погрешности. Они отражают остаточные неопределенности в расчетах. Пришлось пойти на некоторые компромиссы и приближения в связи с конечной — хотя и фантастически большой — вычислительной мощностью компьютера, которая была доступна.
Важным моментом на этом рисунке является точка с надписью N. N означает нуклон, то есть протон или нейтрон. (В масштабе данного рисунка их массы неразличимы.) КХД успешно определяет массы протонов и нейтронов, исходя из первых принципов. В свою очередь, масса в протонах и нейтронах составляет большую часть массы материи. Я обещал объяснить происхождение 95 % массы. Вот оно.



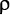 -мезонам (ро-мезонам), Δ-барионам (дельта-барионам) и их сородичам.
-мезонам (ро-мезонам), Δ-барионам (дельта-барионам) и их сородичам.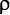 , Δ и другие частицы.
, Δ и другие частицы.
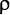 , K*,
, K*,
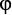 . Третий и четвертый столбцы — это барионы со спином 1/2: N, K; и спином 2/3: Δ, Ω соответственно. Пятый и шестой столбцы — это мезоны чармоний и боттомоний с различными спинами. Эти мезоны интерпретируются как связанные состояния тяжелого (очарованного) кварка с и его антикварка или соответственно (нижнего) кварка b и его антикварка. В этих столбцах высоты представляют собой массовые различия между частицей, о которой идет речь, и легчайшим состоянием чармония или боттомония
. Третий и четвертый столбцы — это барионы со спином 1/2: N, K; и спином 2/3: Δ, Ω соответственно. Пятый и шестой столбцы — это мезоны чармоний и боттомоний с различными спинами. Эти мезоны интерпретируются как связанные состояния тяжелого (очарованного) кварка с и его антикварка или соответственно (нижнего) кварка b и его антикварка. В этих столбцах высоты представляют собой массовые различия между частицей, о которой идет речь, и легчайшим состоянием чармония или боттомония