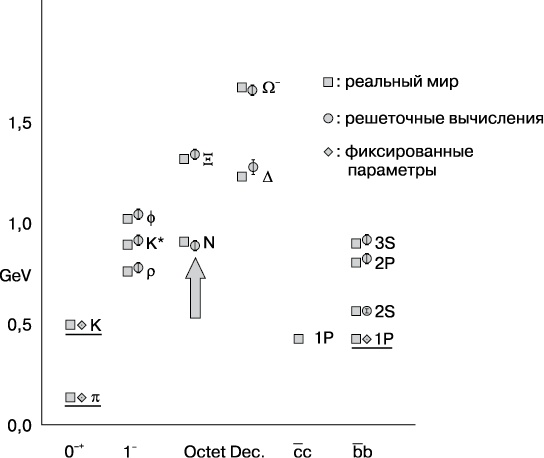
Рис. 9.3. Успешное сравнение наблюдаемых и предсказанных значений спина и массы частиц
Примечательным также является то, чего компьютер не выдает. Нет дополнительных кругов, соответствующих спрогнозированным частицам, которые в результате не были обнаружены. Особо следует подчеркнуть то, что, хотя основными входными данными для расчета являются кварки и глюоны, они не присутствуют среди выходных данных! Принцип конфайнмента, который казался таким странным и отчаянным, здесь играет роль примечания к полному и всеобъемлющему соответствию реальности.
Конечно, вычислять — или использовать для этого гигантский сверхбыстрый компьютер — не значит понимать. Понимание — это задача следующей главы.
Тем не менее, прежде чем закончить эту главу, я хотел бы остановиться на неброском рис. 9.3 и отдать должное группе его авторов. С помощью сложных расчетов, требующих строжайшей точности и всей мощи современных компьютерных технологий, они показали, что непреклонные уравнения высокой симметрии убедительно и в количественном отношении точно объясняют существование протонов и нейтронов, а также их свойства. Они продемонстрировали происхождение массы протона и, таким образом, происхождение львиной доли нашей массы. Я считаю это одним из величайших научных достижений всех времен.
Глава 10. Происхождение массы
Умение что-то вычислить не равнозначно пониманию. Компьютерные вычисления происхождения массы могут быть убедительными, но этого мало. К счастью, мы можем понять происхождение массы.
Ответы, полученные в результате трудоемких и непрозрачных компьютерных вычислений, не удовлетворяют нашу жажду понимания. А что могло бы ее удовлетворить?
Поль Дирак славился своей молчаливостью, но то, что он говорил, часто обладало глубоким смыслом. Однажды он сказал: «Я чувствую, что понимаю уравнение, когда я могу предвидеть поведение его решений, не решая его».
В чем ценность такого понимания?
«Решение» уравнений — это лишь один из инструментов работы с ними, и не самый совершенный. Расчеты, которые мы обсуждали в предыдущей главе, являются поучительным примером. Они убедительно показывают, что уравнения для кварковой и глюонной Сетки точно учитывают массы протонов, нейтронов и других адронов. Они также показывают, что эти уравнения скрывают кварки и глюоны. (Вы можете использовать невозможность существования изолированных кварков или глюонов для вычисления их массы, когда вы учитываете их облака виртуальных частиц — ответом является бесконечность!)
Те славные результаты были достигнуты благодаря героическим усилиям человека и машины. Однако потребность в героизме является одним из самых больших недостатков подхода, подразумевающего «решение» уравнений. Мы не хотим тратить дорогие ресурсы компьютера и долго ждать ответа каждый раз, когда задаем немного другой вопрос. Что еще важнее, мы не хотим тратить дорогие ресурсы компьютера и очень долго ждать ответа, когда мы задаем более сложные вопросы. Например, мы бы хотели иметь возможность предсказывать массы не только отдельных протонов и нейтронов, но и систем, содержащих несколько протонов и нейтронов — атомных ядер. В принципе, у нас есть для этого уравнения, но их решение является нецелесообразным. Мы имеем адекватные уравнения для ответа на любой вопрос химии. Однако от этого химики не лишились работы и не были заменены компьютерами, поскольку эти расчеты слишком сложны.
В случае как ядерной физики, так и химии мы готовы пожертвовать чрезвычайной точностью ради простоты использования и гибкости. Вместо того чтобы «решать» уравнения, перемалывая числа, мы создаем упрощенные модели и выводим эмпирические правила, которые могут предоставить нам практическое руководство в сложных ситуациях. Эти модели и эмпирические правила могут вырасти из опыта решения уравнений, и их можно проверить путем решения уравнений, когда это целесообразно, однако они живут своей собственной жизнью. Это напоминает мне о различии между аспирантами и профессорами: аспирант знает все ни о чем, а профессор ничего не знает обо всем. Решение уравнений — это удел аспирантов, понимание — удел профессоров.
Мы бываем бесконечно далеки от понимания, когда при решении уравнений обнаруживаем поведение, которое является совершенно неожиданным и похожим на чудо. Компьютеры дали нам массу — и не просто массу, а нашу массу, массу составляющих нас протонов и нейтронов — из кварков и глюонов, которые сами по себе массы не имеют (или почти не имеют). В результате решения уравнений КХД получается масса без массы. Это звучит подозрительно, как нечто из ничего. Как это случилось?
К счастью, мы можем получить приблизительное понимание этого кажущегося чуда. Для этого нам требуется собрать вместе три идеи, которые мы уже обсуждали по отдельности. Давайте освежим их в памяти.
Первая идея: цветущие бури
Цветной заряд кварка обеспечивает возмущение Сетки — конкретно в глюонных полях, — которое растет с увеличением расстояния. Это похоже на странное облако, которое распускается из прозрачного центра, превращаясь в зловещую грозовую тучу. Возмущение полей означает их перевод в состояние более высокой энергии. Для возмущения полей в бесконечном объеме требуется бесконечная энергия. Думаю, даже Exxon Mobil не будет утверждать, что у Природы достаточно ресурсов, чтобы заплатить такую цену
[39] Таким образом, кварки не могут существовать в свободном состоянии.
Вторая идея: дорогостоящая компенсация
Цветущую бурю можно прекратить, поместив рядом с кварком антикварк с противоположным цветным зарядом. В этом случае два источника возмущения нейтрализуют друг друга и покой восстановится.
Если бы антикварк был расположен точно над кварком, компенсация была бы полной. При этом произошло бы минимально возможное возмущение в глюонных полях, то есть никакого. Однако у такой точной компенсации есть еще одна цена, обусловленная квантово-механической природой кварков и антикварков.
Согласно принципу неопределенности Гейзенберга, если вы хотите иметь точное знание о положении частицы, вам необходимо допустить широкий разброс в значении ее импульса. В частности, вы должны допустить, что частица может иметь большой импульс. Но большой импульс означает большую энергию. И чем более точно вы зафиксируете положение частицы (локализуете ее, выражаясь научными терминами), тем больше энергии вам придется на это потратить.
(Цветной заряд кварка также можно нейтрализовать, используя дополнительные цветные заряды двух других кварков. Это то, что происходит с барионами, в том числе с протоном и нейтроном, в отличие от мезонов, основанных на паре «кварк — антикварк». Принцип остается тем же.)



