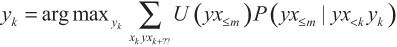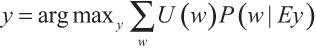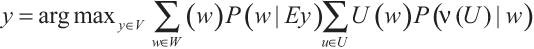Варианты эффекта самостимуляции также могут возникнуть у систем, не стремящихся получить внешнее вознаграждение, то есть у таких, чьи цели предполагают достижение какого-то внутреннего состояния. Скажем, в случае систем «актор–критик», где модуль актора выбирает действия так, чтобы минимизировать недовольство отдельного модуля критика, который вычисляет, насколько соответствует поведение актора требуемым показателям эффективности. Проблема этой системы следующая: модуль актора может понять, что способен минимизировать недовольство критика, изменив или вовсе ликвидировав его — как диктатор, распускающий парламент и национализирующий прессу. В системах с ограниченными возможностями избежать этой проблемы можно просто: не дав модулю актора никаких инструментов для модификации модуля критика. Однако обладающий достаточным интеллектом и ресурсами модуль актора всегда сможет обеспечить себе доступ к модулю критика (который фактически представляет собой лишь физический вычислительный процесс в каком-то компьютере)
[464].
Прежде чем перейти к агенту, который проходит обучение ценностям, давайте в качестве промежуточного шага рассмотрим другую систему, максимизирующую полезность на основе наблюдений (ИИ-МНП). Она получается путем замены последовательности подкреплений (rk + … + rm) в ИИ-ОП на функцию полезности, которая может зависеть от всей истории будущих взаимодействий ИИ:
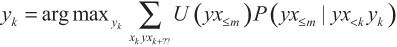
Эта формула позволяет обойти проблему самостимуляции, поскольку функцию полезности, зависящую от всей истории взаимодействий, можно разработать так, чтобы наказывать истории взаимодействия, в которых проявляются признаки самообмана (или нежелания агента прикладывать достаточные усилия, чтобы получить точную картину действительности).
Таким образом, ИИ-МНП дает возможность обойти проблему самостимуляции в принципе. Однако, чтобы ею воспользоваться, нужно задать подходящую функцию полезности на классе всех возможных историй взаимодействия — а это очень трудная задача.
Возможно, более естественным было бы задать функцию полезности непосредственно в терминах возможных миров (или свойств возможных миров, или теорий о мире), а не в терминах историй взаимодействия агента. Используя этот подход, формулу оптимальности ИИ-МНП можно переписать и упростить:
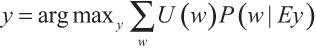
Здесь E — это все свидетельства, доступные агенту (в момент, когда он принимает решение), а U — функция полезности, которая присваивает полезность некоторому классу возможных миров. Оптимальный агент будет выбирать действия, которые максимизируют ожидаемую полезность.
Серьезная проблема этих формул — сложность задания функции полезности. И это наконец возвращает нас к проблеме загрузки ценностей. Чтобы функцию полезности можно было получить в процессе обучения, мы должны расширить наше формальное определение и допустить неопределенность функции полезности. Это можно сделать следующим образом (ИИ-ОЦ)
[465]:
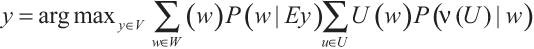
где v(—) — функция от функций полезности для предположений относительно функций полезности. v(U) — предположение, что функция полезности U удовлетворяет критерию ценности, выраженному v
[466]
То есть чтобы решить, какое действие выполнять, нужно действовать следующим образом: во-первых, вычислить условную вероятность каждого возможного мира w (учитывая все возможные свидетельства и исходя из предположения, что должно быть выполнено действие y); во-вторых, для каждой возможной функции U вычислить условную вероятность того, что U удовлетворяет критерию ценности v (при условии, что w — это реальный мир); в-третьих, для каждой возможной функции полезности U вычислить полезность возможного мира w; в-четвертых, использовать все эти значения для расчета ожидаемой полезности действия y; в-пятых, повторить эту процедуру для всех возможных действий и выполнить действие, имеющее самую высокую ожидаемую полезность (используя любой метод выбора из равных значений в случае возникновения таковых). Понятно, что таким образом описанная процедура — предполагающая явное рассмотрение всех возможных миров — вряд ли реализуема с точки зрения потребности в вычислительных ресурсах. ИИ придется использовать обходные пути, чтобы аппроксимировать это уравнение оптимальности.