Этот вывод представляется нам несколько неожиданным, так как мы интуитивно предполагаем, что все числа имеют равные шансы на появление. Безусловно, если поместить в ящик 999 шариков для пинг-понга, пронумерованных от 1 до 999, и извлекать их в произвольном порядке, то вероятность выбора любого числа с определенной цифрой в начале составляет одну девятую, или 11 процентов. Другими словами, у всех цифр в этом случае одинаковые перспективы. Однако очевидно и то, что в газетах первые цифры чисел ведут себя абсолютно иначе: они распределены по явно выраженному асимметричному закону.
Тенденцию к преобладанию чисел, начинающихся с единицы, впервые заметил американский астроном канадского происхождения Саймон Ньюком
[36]. В 1881 году он опубликовал в журнале American Journal of Mathematics краткую заметку, в которой объяснял, что выявил данную особенность благодаря книгам с логарифмическими таблицами. Первые страницы с таблицами логарифмов для чисел, начинающихся с цифры 1, всегда были более истрепаны, чем страницы с таблицами для чисел, начинающихся с цифры 9. Подобный феномен уж точно не объяснишь тем, что исследователи якобы внимательно читали первые страницы книги, а затем теряли к ней интерес из-за отсутствия захватывающего сюжета. Здесь причина в другом: они чаще сталкивались в работе с числами, начинающимися с единицы. Ньюком предположил, что частотность первых цифр чисел, выраженная в процентах, примерно такова.
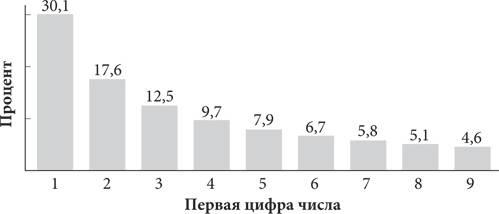
Частота наличия цифры 1 в начале чисел составляет 30,1 процента, цифры 2 — 17,6 процента, цифры 3 — 12,5 процента, причем этот показатель стремительно падает по мере увеличения цифры: шанс встретить цифру 1 в начале чисел в семь раз превышает подобную вероятность по отношению к цифре 9.
Ньюком рассчитал эти показатели с помощью логарифмов. Он утверждал, что вероятность появления цифры d в начале числа определяется по формуле: log(d + 1) — log d. (В Приложении 1 я объясню ее суть.) Однако он не смог четко обосновать ее, поэтому привел вместо этого неформальный аргумент, просто представив его как некую любопытную тенденцию.
Более чем полвека спустя, в 1938 году, физик из General Electric Фрэнк Бенфорд заново открыл феномен первой цифры, тоже обратив внимание на потрепанность страниц в книгах с таблицами логарифмов (по всей вероятности, он не знал о статье Ньюкома)
[37]. Однако Бенфорд проанализировал эту закономерность не только на основании книг с логарифмами. Он изучил распределение первых цифр исходя из таких данных, как население городов США, адреса первых нескольких сотен людей из биографического справочника американских ученых American Men of Science, атомный вес химических элементов, площадь бассейна рек и статистика бейсбольных матчей. В большинстве случаев результаты были близки к ожидаемому распределению. Наверное, было очень интересно наблюдать за тем, как одна и та же последовательность возникает в самых разных ситуациях. Разумеется, полученные показатели не были в точности такими, как представленные выше проценты (в реальном мире подобной точности нет). Тем не менее в целом они почти полностью совпадали с прогнозируемыми значениями, отклоняясь от них не более чем на несколько десятых процента. В настоящее время закон Бенфорда нашел свое подтверждение в самых разных областях, в том числе в естествознании, финансах, экономике и вычислительной технике. Этот закон гласит: в любом множестве данных о естественных произвольных процессах, включающем в себя величины нескольких порядков, частота появления цифры 1 в качестве первой значащей цифры составляет около 30 процентов, цифры 2 — около 18 процентов и т. д. Бенфорд считал, что этот феномен отражает универсальный закон, который он обозначил термином «закон аномальных чисел». Но термин не прижился, и открытие получило известность под названием «закон Бенфорда».
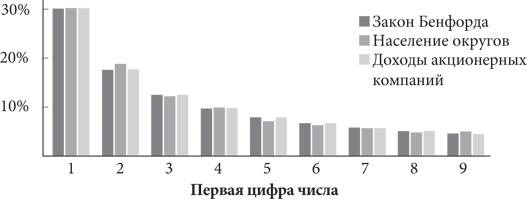
Закону Бенфорда подчиняется большинство множеств данных, взятых из реальной жизни, например численность населения в 3221 округе США и совокупный квартальный доход 30 525 открытых акционерных компаний за период с 1961 по 2011 год
[38].
Закон Бенфорда — одна из самых замечательных числовых закономерностей, существующих в мире. Чуть ниже я остановлюсь на некоторых других, но, прежде чем перейти к ним, мы должны провести одно расследование.
Даррелл Доррелл напоминал мне медведя. Эта ассоциация отчасти объяснялась тем, что мы с ним встретились в Портленде, столице штата Орегон, в котором водится много медведей, и частично тем, что Даррелл был мужчиной коренастого телосложения, с торчащими усами и низким голосом, смахивающим на тихое рычание. Кроме того, ассоциация была связана с его работой финансового следователя. Даррелл вынюхивает искаженные данные с хищническим инстинктом гризли, добывающего себе пищу. Вам лучше не допускать его к своим бухгалтерским книгам, если в них есть хотя бы малейший намек на злоупотребления. ЦРУ, Министерство юстиции и Комиссия по ценным бумагам и биржам регулярно пользовались его услугами в области судебно-бухгалтерской экспертизы (этим отраслевым термином обозначается расследование финансовых махинаций). У Даррелла есть лицензия на ношение оружия. «Все двери здесь закрываются изнутри, — объяснял он. — Мы вызываем у многих людей недовольство».
Когда в начале тысячелетия Даррелл впервые услышал о законе Бенфорда, он испытал примерно те же эмоции, что и люди, пережившие большую утрату: удивление, отрицание, гнев и принятие. «Сначала у меня возникла мысль: “Почему я не слышал об этом раньше?” Затем я подумал: “Этого просто не может быть!” А когда в конце концов понял суть этого закона, на меня снизошло озарение: “Вот это да! Ведь это еще один инструмент, который можно использовать”». Теперь в ходе расследования финансовых махинаций Даррелл прежде всего проверяет первые цифры номеров банковских счетов и данных в бухгалтерских книгах компаний. Финансовые данные, включающие в себя величины нескольких порядков (другими словами, которые отражают количество, измеряемое в единицах продукции или в десятках, сотнях и тысячах долларов), должны подчиняться закону Бенфорда. Если этого не происходит, значит, либо существует обоснованное объяснение (например, регулярная закупка товаров стоимостью, скажем, 40 долларов за единицу, которая влечет за собой повышение вероятности появления цифры 4), либо имеют место преступные действия. Отклонение от закона Бенфорда — это признак того, что соответствующие финансовые данные требуют более тщательного анализа.




