Его можно преобразовать так:
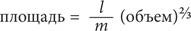
А это уравнение можно отнести к следующему типу:
y = kxa,
где x и y — переменные, а k и a — константы.
Уравнение данного типа также называется степенным законом. Когда степенной закон выражен в такой форме, говорят, что переменная y находится в прямой пропорциональной зависимости от xa, а когда он представлен в виде уравнения
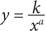 , о котором шла речь выше, переменная y находится в обратной пропорциональной зависимости от xa.
, о котором шла речь выше, переменная y находится в обратной пропорциональной зависимости от xa.
График уравнения степенного закона y = x⅔ размещен ниже. На первом графике в нормальном масштабе кривая по мере повышения выравнивается. Если y — это площадь, а x — объем, то это показывает, что по мере увеличения объема площадь тоже увеличивается, но не так быстро. На графике в двойном логарифмическом масштабе (второй график) степенной закон, отражающий прямо пропорциональную зависимость, дает прямую линию с наклоном вправо.
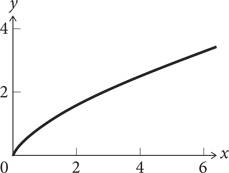
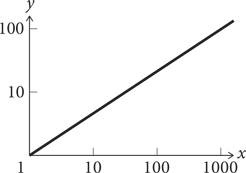
Кривая y = x⅔ на графике в простом и двойном логарифмическом масштабе
Уравнение степенной зависимости между объемом и площадью обозначается также термином «закон масштабирования», поскольку оно демонстрирует, что происходит с измеримой величиной объекта (в данном случае площадью поперечного сечения) в результате увеличения общего размера.
В 30-х годах ХХ столетия швейцарский зоолог Макс Клайбер измерил вес нескольких видов млекопитающих и их уровень метаболизма (минимальное количество энергии, вырабатываемое животными в состоянии покоя)
[53]. Когда ученый отобразил полученные данные на графике в двойном логарифмическом масштабе, получилась прямая линия, на основании которой он вывел следующий степенной закон:
скорость обмена веществ ≈ 70 (масса)¾
Этот закон известен как закон Клайбера. Впоследствии биологи расширили его действие на всех теплокровных животных, как показано на представленном ниже рисунке. Скорость обмена веществ растет не так быстро, как масса, а это говорит о том, что чем крупнее животные, тем эффективнее они вырабатывают энергию. Было также выявлено, что жизнь животных подчиняется и многим другим законам масштабирования. Например, продолжительность жизни животных прямо пропорциональна массе в степени ¼, а частота сердечных сокращений обратно пропорциональна массе в степени ¼. Поскольку коэффициент степенного закона — это в большинстве случаев величина, кратная ¼, биологические степенные законы называют законами четвертного степенного масштабирования. Учитывая разнообразие животного мира (размер млекопитающих колеблется от этрусской мыши весом около одного грамма до голубого кита, который в 100 миллионов раз тяжелее), действительно замечательно, что информация о размере животного позволяет так много сказать о нем.
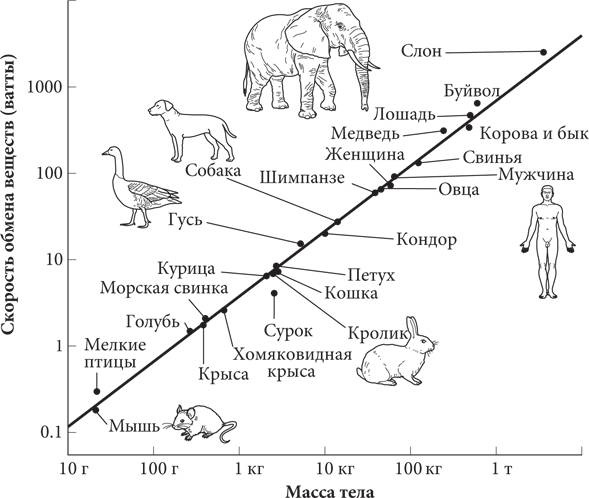
Закон Клайбера
Физик Джеффри Уэст из Института Санта-Фе и биологи Джеймс Браун и Брайан Энквист из Университета Нью-Мексико разработали математическую теорию, которая объясняет эффект четвертного степенного масштабирования
[54] Если в общих чертах, то они утверждают, что при рассмотрении любого организма как транспортной системы (кровь поступает в аорту, разветвляющуюся на артерии, которые, в свою очередь, разветвляются на более узкие кровеносные сосуды) ее оптимизация под имеющееся пространство порождает степенной закон. Подробное объяснение данного феномена выходит за рамки материала этой книги, но представляет интерес в данном контексте в связи с другой работой Уэста — изучением организма иного типа: города.
Уэст и его коллеги обнаружили, что масштабирование по степенному закону весьма характерно для маленьких и больших городов
[55]. Проанализировав огромное количество экономических и социальных данных и отобразив полученные результаты на графиках в двойном логарифмическом масштабе, они установили, что в США имеют место следующие закономерности:
количество изобретателей = k (численность населения)1,25
совокупная заработная плата = k (численность населения)1,12
количество случаев заболевания СПИДом = k (численность населения)1,23
количество тяжких преступлений = k (численность населения)1,16
В этих уравнениях показатель степени (экспонента) больше 1, а это значит, что чем крупнее город, тем в нем больше изобретателей, совокупной заработной платы, случаев заболеваний СПИДом и тяжких преступлений на душу населения. Здесь налицо пропорциональная зависимость. По всем этим городским индикаторам значение показателей степени составляет примерно 1,2, и такая сосредоточенность вокруг одного значения интересна сама по себе. Исходя из этого, получается, что при увеличении размера города вдвое можно ожидать роста количества изобретателей, совокупной заработной платы, случаев заболеваний СПИДом и тяжких преступлений на душу населения на 15 процентов.
В случае ряда других городских индикаторов показатель степени меньше 1, а это значит, что рост города может привести к сокращению следующих показателей на душу населения:
количество автозаправочных станций = k (численность населения)0,77



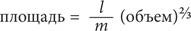
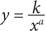 , о котором шла речь выше, переменная y находится в обратной пропорциональной зависимости от xa.
, о котором шла речь выше, переменная y находится в обратной пропорциональной зависимости от xa.

