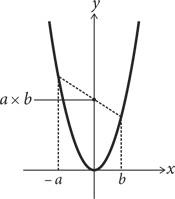
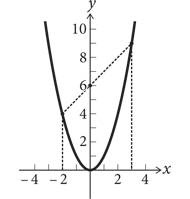
Мебиус хорошо разбирался в геометрических изгибах: в буквальном смысле слова, как в случае ленты Мебиуса (скрученной полоски бумаги со склеенными концами), и в более абстрактном смысле — при вычислениях с помощью параболы. Этот метод представлен ниже на первом рисунке. Для того чтобы выполнить операцию a × b, достаточно нарисовать прямую линию между точками на параболе, где x = —a и x = b. Точка, в которой эта линия пересекает ось у, — и есть ответ! Все, что нужно, — это нарисовать линию и отметить точку пересечения. На рисунке справа — пример выполнения операции 2 × 3. Требуемая линия проходит через точки на параболе, в которых x = –2 и x = 3, и пересекает ось у в точке 6. Данный метод применим к любым двум числам (доказательство можно найти в Приложении 4).
Как умножить два числа с помощью параболы
Мебиус представил свою оригинальную машину умножения в 1841 году в ссылке к статье, опубликованной в августовском номере журнала Journal für die reine und angewandte Mathematik («Журнал чистой и прикладной математики»), и больше никогда не упоминал об этом методе. Однако идею решения арифметических задач с помощью геометрии впоследствии переосмыслил молодой французский математик Морис д’Окань
[87]. Он обнаружил, что кроме операции умножения можно, построив прямую линию между двумя точками на графике и записав ответ, выполнять и многие другие операции. В 1891 году д’Окань ввел термин «номограмма» для обозначения любой таблицы, которую можно использовать для таких вычислений, и сам составил множество таких таблиц. Каждая номограмма подходит для вычислений лишь по одной формуле. На представленном ниже рисунке изображена составленная в 1921 году номограмма для формулы расчета скорости перемещения потока воды через прямоугольное отверстие в плотине, где V — это скорость потока, h1 и h2 — высота верхнего и нижнего края отверстия. Прямая линия, проведенная через точки h1 и h2, пересечется с вертикальной линией в точке, соответствующей искомому значению V. Все, что необходимо для решения этого громоздкого уравнения, — линейка и твердая рука. Номограммы помогли избавиться от трудоемких вычислений, затратных по времени. Они широко применялись в инженерном и военном деле до 1970-х годов, когда электронный калькулятор в одночасье сделал их устаревшими. Гениальные, практические и зачастую красивые номограммы вышли из употребления, а номография стала забытым искусством.
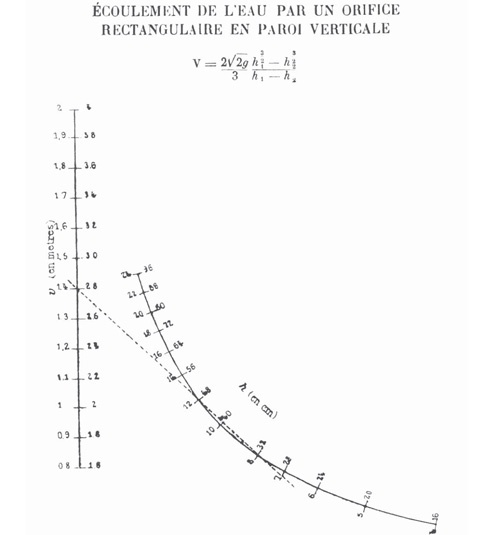
До изобретения карманного калькулятора широко использовались вспомогательные вычислительные инструменты под названием «номограммы». Эта номограмма, составленная в 1921 году, вычисляет скорость потока воды в водосливе плотины
Из книги: Rodolphe Soreau, Nomographie, Chiron, 1921
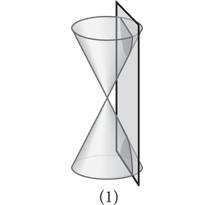
Гипербола выделяется на фоне остальных конических сечений, поскольку состоит из двух частей. Для того чтобы понять, почему так происходит, мы должны вернуться к первоначальному определению конических сечений. Если нарисовать рисунок, отображающий весь процесс построения гиперболы, то на нем было бы видно, что на самом деле наш нож рассекает двойной конус, когда один конус расположен в перевернутом виде над другим идентичным конусом
[88]. В случае эллипса и параболы угол наклона секущей плоскости указывает, что эта плоскость никогда не достигнет верхнего конуса. Хотя, как показано на рисунке 1 ниже, в случае гипербол секущие плоскости всегда пересекают как верхний, так и нижний конусы, образуя при этом две симметричные U-образные ветви.
Благодаря гиперболе в геометрии появилась совершенно новая концепция — асимптота (еще один термин, введенный Аполлонием), прямая линия, к которой другая кривая приближается бесконечно близко, но никогда с ней не соприкасается. Как показано на рисунке 2, гипербола ограничена двумя пересекающимися асимптотами. Каждый незамкнутый фрагмент кривой постоянно приближается к асимптоте, но никогда не пересекается с ней. «Я уверен, что если бы геометр сознавал безнадежное и отчаянное стремление гиперболы соединиться со своими асимптотами, — писал испанский философ Мигель де Унамуно, — то он охарактеризовал бы гиперболу как живое и трагическое существо!» Гиперболы часто встречаются в быту. Как показано на рисунках 3 и 4, это могут быть дугообразные волны на заточенном карандаше (кончик — это конус, а плоская боковая сторона — секущая плоскость), а также тень, отбрасываемая лампой (пучок лучей света — это конус, а стена — секущая плоскость).
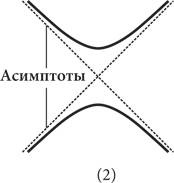
Гиперболы Асимптоты
У гиперболы два фокуса, как и у эллипса. Ее можно представить себе как эллипс, вытянутый до бесконечности в одном направлении, а затем развернутый в обратном направлении. Кроме того, гиперболу можно определить по свойствам двух ее фокусов, как это было сделано и в отношении эллипса. Гипербола — это путь, пройденный точкой, расстояния от которой до двух фокусов образуют постоянную разность, тогда как в случае эллипса они образуют постоянную сумму. На верхнем рисунке a — это расстояние от произвольной точки P до одного фокуса, а b — расстояние от точки P до другого фокуса. Гипербола — это геометрическое место точки P, для которой разность (a — b) имеет постоянное значение. Кроме того, гиперболу можно определить и через поведение лучей света. Лучи света от источника, находящегося в одном из фокусов, отражаются вовне гиперболического зеркала в направлении, противоположном другому фокусу, как показано на нижнем рисунке. Телескоп Ричи-Кретьена, наиболее распространенный тип больших астрономических телескопов, содержит именно гиперболические зеркала.









