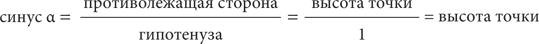Перекатывание монет
Когда мне задали этот вопрос впервые, я предположил, что монета окажется в перевернутом положении, поскольку она прошла только половину пути вокруг неподвижной монеты. Но я ошибался. Королева делает полный оборот, что на первый взгляд противоречит здравому смыслу. Монета с королевской скоростью перемещается вокруг другой монеты, как будто отчаянно пытаясь сохранить достоинство, снова заняв строго вертикальное положение. Дело в том, что траектория движения монеты формируется благодаря свойству, присущему всем рулеттам: они представляют собой результат движения в двух независимых направлениях. В данном примере монета вращается вокруг себя и вокруг другой монеты. На каждый градус перемещения левой монеты вокруг правой приходится два градуса ее вращения вокруг себя.
Рулетты образуются в случае подвижного колеса. Однако кривые можно получить и посредством вращения колеса вокруг неподвижного центра. Такие кривые проще рулетт, поскольку формируются благодаря движению только в одном направлении — вокруг центра.
Возьмем точку на ободе колеса, вращающегося против часовой стрелки, как показано на рисунке 1 ниже. Если нанести на график высоту этой точки в зависимости от угла поворота, отмеченного на горизонтальной оси, получится кривая под названием синусоида, или синусоидальная волна. Я указал на рисунке положение точки при угле поворота 0, 45, 90, 225 и 270 градусов. Синусоида достигает максимума, когда угол поворота составляет 90 градусов, затем возвращается к горизонтальной оси при 180 градусах, после чего опускается ниже горизонтальной оси, а когда точка совершает полный оборот, возвращается в исходное положение. Если колесо продолжит вращаться, кривая будет повторяться с каждым новым оборотом, создавая симметричные волнообразные колебания до бесконечности.
Наверное, вам интересно знать, почему у названия этой волнистой линии один корень со словом «синус», которым обозначается соотношение между двумя сторонами прямоугольного треугольника, ведь между волнами и треугольниками нет ничего общего. Однако все это обретает смысл, если мы вспомним, что концепция синуса связана, прежде всего, с окружностью: это не что иное, как полухорда, что прекрасно видно на рисунке 2, где в окружности размещен прямоугольный треугольник. Предположим, длина гипотенузы равна 1, тогда синус угла α рассчитывается по формуле:
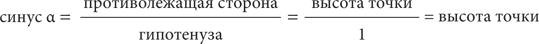
Первым синусоиду нарисовал Жиль де Роберваль в XVII столетии и назвал ее «кривой, сопутствующей циклоиде»
[98]. Эта «спутница» займет впоследствии исключительное место в сердцах (и мыслях) ученых и математиков.
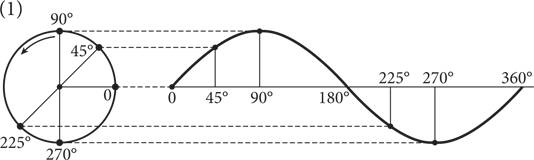
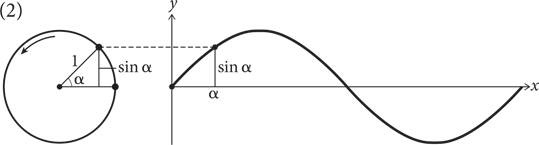
Изменение высоты вращающейся точки по отношению к углу поворота порождает синусоидальную волну
Синусоида — это кривая, которую называют периодической волной, поскольку она повторяется вдоль горизонтальной оси снова и снова. Синусоида — простой тип периодических волн, так как образующая ее окружность является простейшей геометрической фигурой. Однако, несмотря на то что синусоида представляет собой базовую концепцию, она моделирует множество физических явлений. Мир — настоящий карнавал синусоид. Изменяющееся во времени вертикальное положение груза, перемещающегося вместе с пружиной вверх и вниз, — это синусоида, как показано на левом рисунке ниже
[99]. Груз движется с максимальной скоростью в середине периода колебания и замедляет движение в момент достижения верхней и нижней точек, что создает легко узнаваемую кривую (на рисунке отображено небольшое количество колебаний, ввиду того что горизонтальная ось здесь ограничена). Изменяющееся во времени горизонтальное положение маятника, колеблющегося из стороны в сторону с небольшой амплитудой, тоже образует синусоиду. Представьте себе, что шар маятника наполнен мелким песком и он просачивается через отверстие в нижней точке шара, как показано на рисунке снизу. Маятник, качающийся с севера на юг, оставит след в виде синусоидальной волны на ленте конвейера, движущейся с востока на запад. Говорят, что такие объекты, как пружина и маятник, колебания которых изменяются с течением времени по синусоидальному закону, совершают простое гармоническое колебание.
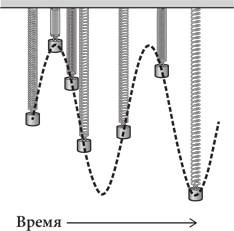
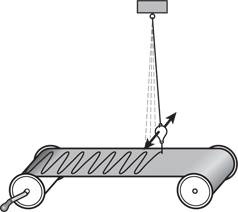
Подвешенный на пружине груз и колеблющийся маятник совершают простое гармоническое колебание
Мы уже видели, какие красивые рисунки образуют рулетты. То же самое можно сказать и о синусоидах. В 1840-х годах шотландский математик Хью Блэкберн экспериментировал с маятником, шар которого был наполнен песком. Он решил подвесить этот шар на двух шнурах, свисающих в форме буквы Y и прикрепленных друг к другу кольцом в точке r, как показано на рисунке ниже. Удерживая кольцо в неподвижном состоянии, Блэкберн качнул маятник слева направо. Затем он отпустил кольцо и толкнул его вперед, тем самым создав колебание вперед-назад. Таким образом, шар маятника двигался под воздействием двух перпендикулярных колебаний, что давало весьма впечатляющий результат. Эти два конкурирующих синусоидальных колебания отталкивали и притягивали друг друга, совершая своего рода математическое па-де-де, вычерчивающее под маятником удивительно замысловатый рисунок из песка. Через какое-то время предприимчивые производители инструментов начали выпускать устройства под названием «гармонографы», в которых два маятника совершают колебания пишущим пером в двух направлениях одновременно. Пользователь гармонографа мог скорректировать длину маятников, установить амплитуду их колебаний, а затем отпустить, разместив перо над листом бумаги. Перо начинало вращаться и делать петли, воспроизводя прекрасные геометрические формы, которые, несмотря на механическую природу, почему-то казались живыми.